


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-2-2020
Date: 6-2-2020
Date: 8-2-2020
|
A positive integer 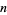 is called a base-
is called a base-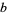 Rhonda number if the product of the base-
Rhonda number if the product of the base-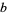 digits of
digits of 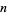 is equal to
is equal to 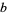 times the sum of
times the sum of 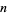 's prime factors. These numbers were named by K. S. Brown after an acquaintance of his whose residence number 25662 satisfies this property. The etymology of the term is therefore similar to the Smith numbers.
's prime factors. These numbers were named by K. S. Brown after an acquaintance of his whose residence number 25662 satisfies this property. The etymology of the term is therefore similar to the Smith numbers.
25662 is a Rhonda number to base-10 since its prime factorization is
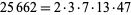 |
(1) |
and the product of its base-10 digits satisfies
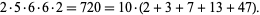 |
(2) |
The Rhonda numbers to base 10 are 1568, 2835, 4752, 5265, 5439, 5664, 5824, 5832, 8526, 12985, ... (OEIS A099542). The corresponding sums of prime factors are 24, 24, 28, 30, 54, 72, 32, 24, 48, 72, ... (OEIS A099543).
Rhonda numbers exist only for bases that are composite since there is no way for the product of integers less than a prime 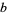 to have
to have 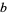 as a factor.
as a factor.
The first few Rhonda numbers for small composite bases 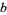 are summarized in the following table.
are summarized in the following table.
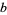 |
OEIS | 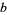 -Rhonda numbers -Rhonda numbers |
| 4 | A100968 | 10206, 11935, 12150, 16031, 45030, 94185, ... |
| 6 | A100969 | 855, 1029, 3813, 5577, 7040, 7304, 15104, 19136, ... |
| 8 | A100970 | 1836, 6318, 6622, 10530, 14500, 14739, 17655, 18550, 25398, ... |
| 9 | A100973 | 15540, 21054, 25331, 44360, 44660, 44733, 47652, ... |
| 10 | A099542 | 1568, 2835, 4752, 5265, 5439, 5664, 5824, 5832, 8526, 12985, ... |
| 12 | A100971 | 560, 800, 3993, 4425, 4602, 4888, 7315, 8296, 9315, 11849, 12028, ... |
| 14 | A100972 | 11475, 18655, 20565, 29631, 31725, 45387, 58404, 58667, 59950, ... |
| 15 | A100974 | 2392, 2472, 11468, 15873, 17424, 18126, 19152, 20079, 24388, ... |
| 16 | A100975 | 1000, 1134, 6776, 15912, 19624, 20043, 20355, 23946, 26296, ... |
The smallest Rhonda number is 560, which is Rhonda to base 12. The integers that are Rhonda numbers to some base are 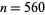 , 756, 800, 855, 1000, 1029, 1134, 1470, 1568, 1632, 1750, 1815, ... (OEIS A100987).
, 756, 800, 855, 1000, 1029, 1134, 1470, 1568, 1632, 1750, 1815, ... (OEIS A100987).
There exist integers that are Rhonda to more than one base. The smallest of these is 1000, which is Rhonda to bases 16 and 36, and the full sequence of these multiply Rhonda numbers begins 1000, 2940, 4200, 4212, 4725, 5670, 5824, ... (OEIS A100988).
That there are infinitely many Rhonda numbers can be seen from the following explicit construction. For any integer 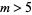 , the number
, the number 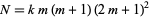 is a Rhonda number to base
is a Rhonda number to base 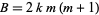 , where
, where 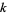 is any integer such that
is any integer such that
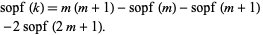 |
(3) |
and 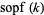 denotes the sum of the prime factors of
denotes the sum of the prime factors of 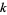 . This equation is guaranteed to have at least one solution for
. This equation is guaranteed to have at least one solution for 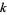 so long as
so long as 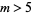 .
.
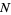 is expressed in base
is expressed in base 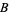 as
as
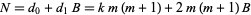 |
(4) |
so the product of the base 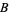 digits of
digits of 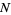 is
is 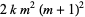 .
.
Because sopf is an additive function, we find that
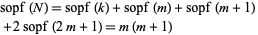 |
(5) |
where in the last step we have made use of (1). Therefore,  times the sum of the prime factors of
times the sum of the prime factors of  is equal to
is equal to 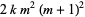 , which is equal to the product of the base
, which is equal to the product of the base 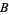 digits of
digits of 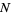 .
.
As an example, let us take 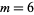 . Then we require that, from (1) above,
. Then we require that, from (1) above,
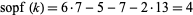 |
(6) |
which is satisfied by 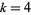 , and so
, and so 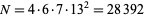 is a Rhonda number to base
is a Rhonda number to base 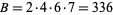 .
.
REFERENCES:
MathPages. "Smith Numbers and Rhonda Numbers." https://www.mathpages.com/home/kmath007.htm.
MathPages. "Infinitely Many Rhondas." https://www.mathpages.com/home/kmath083.htm.
Schneider, W. "Rhonda Numbers." https://www.wschnei.de/digit-related-numbers/rhonda-numbers.html.
Sloane, N. J. A. Sequences A099542, A099543, A100968, A100969, A100970, A100971, A100972, A100973, A100974, A100975, A100987, and A100988 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للتخلص من الإمساك.. فاكهة واحدة لها مفعول سحري
|
|
|
|
|
|
|
العلماء ينجحون لأول مرة في إنشاء حبل شوكي بشري وظيفي في المختبر
|
|
|
|
|
|
|
قسم الشؤون الفكرية يحتفي بإصدار العدد الألف من نشرة الكفيل
|
|
|