


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2018
Date: 24-3-2019
Date: 21-8-2018
|
The Rogers mod 14 identities are a set of three Rogers-Ramanujan-like identities given by
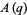 |
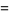 |
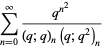 |
(1) |
 |
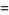 |
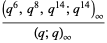 |
(2) |
 |
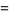 |
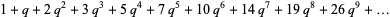 |
(3) |
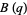 |
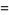 |
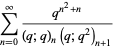 |
(4) |
 |
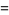 |
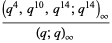 |
(5) |
 |
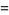 |
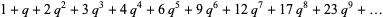 |
(6) |
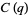 |
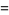 |
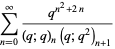 |
(7) |
 |
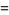 |
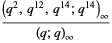 |
(8) |
 |
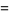 |
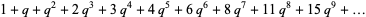 |
(9) |
(OEIS A105780, A105781, and A105782).
The 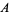 -identity was found by Rogers (1894) and appears as formula 61 in the list of Slater (1952). The
-identity was found by Rogers (1894) and appears as formula 61 in the list of Slater (1952). The 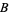 - and
- and 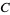 -identities were found by Rogers (1917) and appeared as formulas 60 and 59 respectively in Slater (1952).
-identities were found by Rogers (1917) and appeared as formulas 60 and 59 respectively in Slater (1952).
REFERENCES:
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.
Rogers, L. J. "Second Memoir on the Expansion of Certain Infinite Products." Proc. London Math. Soc. 25, 318-343, 1894.
Rogers, L. J. "On Two Theorems of Combinatory Analysis and Some Allied Identities." Proc. London Math. Soc. 16, 315-336, 1917.
Slater, L. J. "Further Identities of the Rogers-Ramanujan Type." Proc. London Math. Soc. Ser. 2 54, 147-167, 1952.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|