


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2018
Date: 4-8-2019
Date: 19-5-2018
|
The Jackson-Slater identity is the q-series identity of Rogers-Ramanujan-type given by
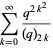 |
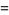 |
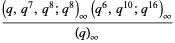 |
(1) |
 |
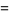 |
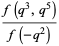 |
(2) |
 |
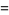 |
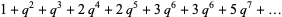 |
(3) |
(OEIS A069910; Leininger and Milne 1999), where 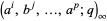 is extended q-series notation and
is extended q-series notation and 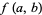 is a Ramanujan theta function.
is a Ramanujan theta function.
The identity in question was actually first published by Jackson (1928) in slightly disguised form as the fifth equation on page 170 in his paper, though this early appearance of this identity is not well-known. It became widely known as equation 39 (and 83) in the collection of identities due to Slater (1952).
REFERENCES:
Jackson, F. H. "Examples of a Generalization of Euler's Transformation for Power Series." Messenger Math. 57, 169-187, 1928.
Leininger, V. E. and Milne, S. C. "Some New Infinite Families of 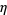 -Function Identities." Methods Appl. Anal. 6, 225-248, 1999.
-Function Identities." Methods Appl. Anal. 6, 225-248, 1999.
Mc Laughlin, J.; Sills, A. V.; and Zimmer, P. "Dynamic Survey DS15: Rogers-Ramanujan-Slater Type Identities." Electronic J. Combinatorics, DS15, 1-59, May 31, 2008. http://www.combinatorics.org/Surveys/ds15.pdf.
Slater, L. J. "Further Identities of the Rogers-Ramanujan Type." Proc. London Math. Soc. Ser. 2 54, 147-167, 1952.
Sloane, N. J. A. Sequence A069910 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|