


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-8-2018
Date: 7-8-2019
Date: 16-5-2018
|
Let 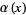 be a step function with the jump
be a step function with the jump
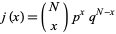 |
(1) |
at 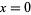 , 1, ...,
, 1, ..., 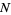 , where
, where 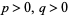 , and
, and 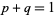 . Then the Krawtchouk polynomial is defined by
. Then the Krawtchouk polynomial is defined by
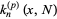 |
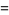 |
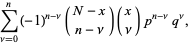 |
(2) |
 |
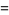 |
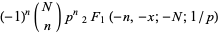 |
(3) |
 |
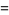 |
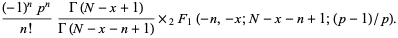 |
(4) |
for 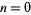 , 1, ...,
, 1, ..., 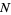 . The first few Krawtchouk polynomials are
. The first few Krawtchouk polynomials are
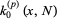 |
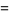 |
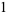 |
(5) |
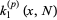 |
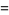 |
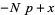 |
(6) |
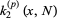 |
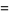 |
![1/2[N^2p^2+x(2p+x-1)-Np(p+2x)].](http://mathworld.wolfram.com/images/equations/KrawtchoukPolynomial/Inline25.gif) |
(7) |
Koekoek and Swarttouw (1998) define the Krawtchouk polynomial without the leading coefficient as
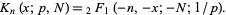 |
(8) |
The Krawtchouk polynomials have weighting function
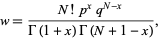 |
(9) |
where 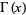 is the gamma function, recurrence relation
is the gamma function, recurrence relation
![(n+1)k_(n+1)^((p))(x,N)+pq(N-n+1)k_(n-1)^((p))(x,N)
=[x-n-(N-2)]k_n^((p))(x,N),](http://mathworld.wolfram.com/images/equations/KrawtchoukPolynomial/NumberedEquation4.gif) |
(10) |
and squared norm
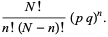 |
(11) |
It has the limit
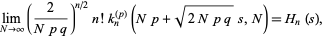 |
(12) |
where 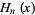 is a Hermite polynomial.
is a Hermite polynomial.
The Krawtchouk polynomials are a special case of the Meixner polynomials of the first kind.
REFERENCES:
Koekoek, R. and Swarttouw, R. F. "Krawtchouk." §1.10 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its 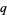 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 46-47, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 46-47, 1998.
Koepf, W. Hypergeometric Summation: An Algorithmic Approach to Summation and Special Function Identities. Braunschweig, Germany: Vieweg, p. 115, 1998.
Nikiforov, A. F.; Uvarov, V. B.; and Suslov, S. S. Classical Orthogonal Polynomials of a Discrete Variable. New York: Springer-Verlag, 1992.
Schrijver, A. "A Comparison of the Delsarte and Lovász Bounds." IEEE Trans. Inform. Th. 25, 425-429, 1979.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 35-37, 1975.
Zelenkov, V. "Krawtchouk Polynomials Home Page." http://www.geocities.com/orthpol/.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|