


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2019
Date: 23-8-2018
Date: 21-8-2018
|
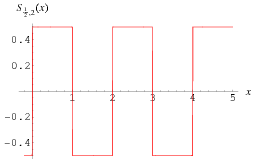
The square wave, also called a pulse train, or pulse wave, is a periodic waveform consisting of instantaneous transitions between two levels. The square wave is sometimes also called the Rademacher function. The square wave illustrated above has period 2 and levels 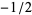 and 1/2. Other common levels for square waves include
and 1/2. Other common levels for square waves include 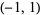 and
and 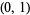 (digital signals).
(digital signals).
Analytic formulas for the square wave 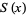 with half-amplitude
with half-amplitude 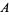 , period
, period 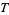 , and offset
, and offset 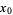 include
include
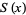 |
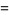 |
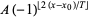 |
(1) |
 |
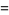 |
![Asgn[sin((2pi(x-x_0))/T)]](http://mathworld.wolfram.com/images/equations/SquareWave/Inline13.gif) |
(2) |
 |
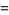 |
![A(2i)/pi[tanh^(-1)(e^(-ipi(x-x_0)/T))-tanh^(-1)(e^(ipi(x-x_0)/T))],](http://mathworld.wolfram.com/images/equations/SquareWave/Inline16.gif) |
(3) |
where 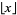 is the floor function,
is the floor function, 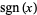 is the sign function, and
is the sign function, and 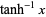 is the inverse hyperbolic tangent.
is the inverse hyperbolic tangent.
The square wave is implemented in the Wolfram Language as SquareWave[x].
Let the square wave have period 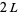 . The square wave function is odd, so the Fourier series has
. The square wave function is odd, so the Fourier series has 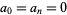 and
and
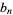 |
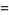 |
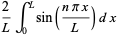 |
(4) |
 |
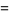 |
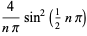 |
(5) |
 |
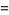 |
![2/(npi)[1-(-1)^n]](http://mathworld.wolfram.com/images/equations/SquareWave/Inline30.gif) |
(6) |
 |
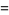 |
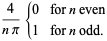 |
(7) |
The Fourier series for the square wave with period 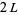 , phase offset 0, and half-amplitude 1 is therefore
, phase offset 0, and half-amplitude 1 is therefore
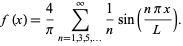 |
(8) |
REFERENCES:
Thompson, A. R.; Moran, J. M.; and Swenson, G. W. Jr. Interferometry and Synthesis in Radio Astronomy. New York: Wiley, p. 203, 1986.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|