


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-3-2017
Date: 23-1-2019
Date: 19-1-2019
|
Eisenstein's irreducibility criterion is a sufficient condition assuring that an integer polynomial 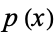 is irreducible in the polynomial ring
is irreducible in the polynomial ring ![Q[x]](http://mathworld.wolfram.com/images/equations/EisensteinsIrreducibilityCriterion/Inline2.gif) .
.
The polynomial
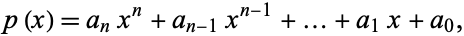 |
where 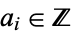 for all
for all 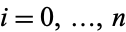 and
and 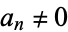 (which means that the degree of
(which means that the degree of 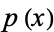 is
is 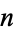 ) is irreducible if some prime number
) is irreducible if some prime number 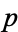 divides all coefficients
divides all coefficients 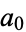 , ...,
, ..., 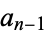 , but not the leading coefficient
, but not the leading coefficient 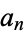 and, moreover,
and, moreover, 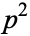 does not divide the constant term
does not divide the constant term 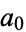 .
.
This is only a sufficient, and by no means a necessary condition. For example, the polynomial 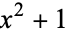 is irreducible, but does not fulfil the above property, since no prime number divides 1. However, substituting
is irreducible, but does not fulfil the above property, since no prime number divides 1. However, substituting 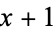 for
for 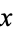 produces the polynomial
produces the polynomial 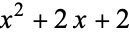 , which does fulfill the Eisenstein criterion (with
, which does fulfill the Eisenstein criterion (with 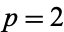 ) and shows the polynomial is irreducible.
) and shows the polynomial is irreducible.
REFERENCES:
Childs, L. A Concrete Introduction to Higher Algebra. New York: Springer-Verlag, pp. 169-172, 1979.
Herstein, I. N. Topics in Algebra, 2nd ed. New York: Wiley, pp. 160-161, 1975.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|