المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Kelvin Transformation |
 587
 02:01 مساءً
date: 27-12-2018 |
Author : Itô, K. (Ed.). 
Book or Source : "Harmonic Functions and Subharmonic Functions: Invariance of Harmonicity." §193B in Encyclopedic Dictionary of Mathematics, 2nd ed. Cambridge 
Page and Part : p. 725|
Read More
Date: 22-6-2018
1714
Date: 12-6-2018
717
Date: 12-6-2018
508
|
Let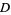 
be a domain in 
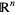for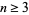 
. Then the transformation
 |
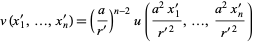onto a domain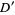 
, where
 |
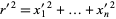is called a Kelvin transformation. If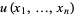 
is a harmonic function on 
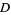, then 
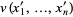is also harmonic on 
.
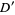REFERENCES:
Itô, K. (Ed.). "Harmonic Functions and Subharmonic Functions: Invariance of Harmonicity." §193B in Encyclopedic Dictionary of Mathematics, 2nd ed. Cambridge, MA: MIT Press, p. 725, 1980.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
