Modified Struve Function

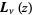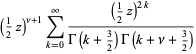			(1)
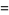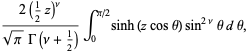			(2)

where 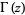 is the gamma function.  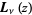is related to the ordinary Struve function  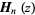by

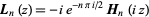(3)

(Abramowitz and Stegun 1972, p. 498).

The Struve function 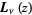 is implemented in the Wolfram Language as StruveL[n, z].

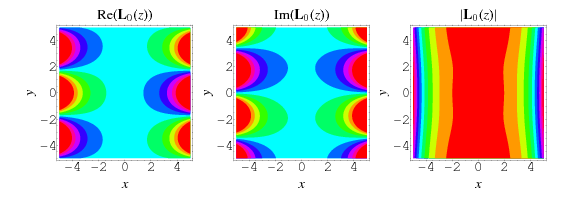
The plots above show 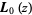 in the complex plane.

REFERENCES:

Abramowitz, M. "Tables of Integrals of Struve Functions." J. Math. Phys. 29, 49-51, 1950.

Abramowitz, M. and Stegun, I. A. (Eds.). "Modified Struve Function 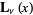." §12.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 498, 1972.

Apelblat, A. "Derivatives and Integrals with Respect to the Order of the Struve Functions 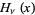 and 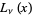." J. Math. Anal. Appl. 137, 17-36, 1999.

Cook, R. K. "Some Properties of Struve Functions." J. Washington Acad. Sci. 47, 365-368, 1957.

Horton, C. W. "On the Extension of Some Lommel Integrals to Struve Functions with an Application to Acoustic Radiation." J. Math. Phys. 29, 31-37, 1950.

Horton, C. W. "A Short Table of Struve Functions and of Some Integrals Involving Bessel and Struve Functions." J. Math. Phys. 29, 56-58, 1950.

Mathematical Tables Project. "Table of the Struve Functions 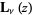 and 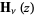." J. Math. Phys. 25, 252-259, 1946.

Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Struve Functions 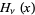 and 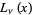." §1.4 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 24-27, 1990.