


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-11-2018
Date: 17-11-2018
Date: 24-10-2018
|
The Jacobi elliptic functions are standard forms of elliptic functions. The three basic functions are denoted 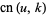 ,
, 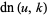 , and
, and 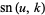 , where
, where 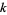 is known as the elliptic modulus. They arise from the inversion of the elliptic integral of the first kind,
is known as the elliptic modulus. They arise from the inversion of the elliptic integral of the first kind,
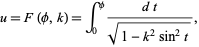 |
(1) |
where 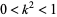 ,
, 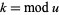 is the elliptic modulus, and
is the elliptic modulus, and 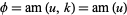 is the Jacobi amplitude, giving
is the Jacobi amplitude, giving
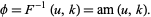 |
(2) |
From this, it follows that
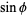 |
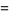 |
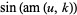 |
(3) |
 |
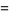 |
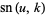 |
(4) |
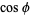 |
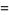 |
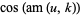 |
(5) |
 |
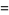 |
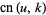 |
(6) |
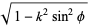 |
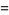 |
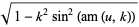 |
(7) |
 |
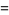 |
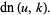 |
(8) |
These functions are doubly periodic generalizations of the trigonometric functions satisfying
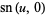 |
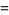 |
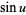 |
(9) |
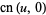 |
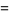 |
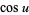 |
(10) |
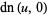 |
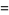 |
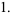 |
(11) |
In terms of Jacobi theta functions,
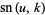 |
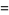 |
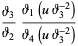 |
(12) |
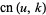 |
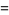 |
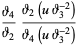 |
(13) |
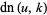 |
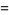 |
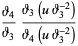 |
(14) |
(Whittaker and Watson 1990, p. 492), where 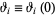 (Whittaker and Watson 1990, p. 464) and the elliptic modulusis given by
(Whittaker and Watson 1990, p. 464) and the elliptic modulusis given by
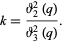 |
(15) |
Ratios of Jacobi elliptic functions are denoted by combining the first letter of the numerator elliptic function with the first of the denominator elliptic function. The multiplicative inverses of the elliptic functions are denoted by reversing the order of the two letters. These combinations give a total of 12 functions: cd, cn, cs, dc, dn, ds, nc, nd, ns, sc, sd, and sn. These functions are implemented in the Wolfram Language as JacobiSN[z, m] and so on. Similarly, the inverse Jacobi functions are implemented as InverseJacobiSN[v, m] and so on.
The Jacobi amplitude 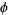 is defined in terms of
is defined in terms of 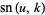 by
by
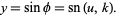 |
(16) |
The 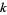 argument is often suppressed for brevity so, for example,
argument is often suppressed for brevity so, for example, 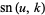 can be written as
can be written as 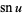 .
.
The Jacobi elliptic functions are periodic in 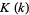 and
and 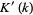 as
as
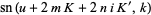 |
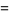 |
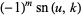 |
(17) |
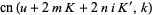 |
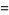 |
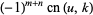 |
(18) |
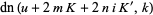 |
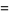 |
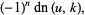 |
(19) |
where 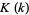 is the complete elliptic integral of the first kind,
is the complete elliptic integral of the first kind, 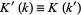 , and
, and 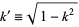 (Whittaker and Watson 1990, p. 503).
(Whittaker and Watson 1990, p. 503).
The 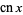 ,
, 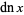 , and
, and 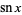 functions may also be defined as solutions to the differential equations
functions may also be defined as solutions to the differential equations
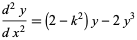 |
(20) |
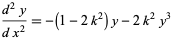 |
(21) |
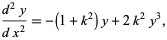 |
(22) |
respectively.
The standard Jacobi elliptic functions satisfy the identities
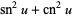 |
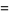 |
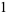 |
(23) |
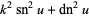 |
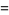 |
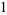 |
(24) |
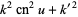 |
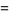 |
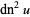 |
(25) |
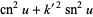 |
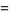 |
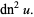 |
(26) |
Special values include
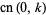 |
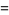 |
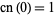 |
(27) |
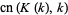 |
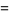 |
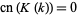 |
(28) |
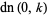 |
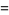 |
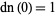 |
(29) |
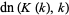 |
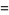 |
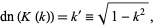 |
(30) |
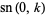 |
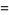 |
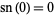 |
(31) |
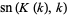 |
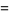 |
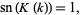 |
(32) |
where 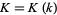 is a complete elliptic integral of the first kind and
is a complete elliptic integral of the first kind and 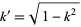 is the complementary elliptic modulus (Whittaker and Watson 1990, pp. 498-499), and
is the complementary elliptic modulus (Whittaker and Watson 1990, pp. 498-499), and
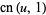 |
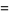 |
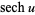 |
(33) |
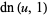 |
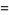 |
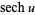 |
(34) |
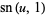 |
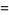 |
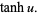 |
(35) |
In terms of integrals,
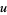 |
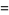 |
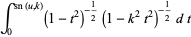 |
(36) |
 |
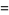 |
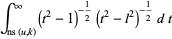 |
(37) |
 |
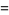 |
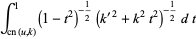 |
(38) |
 |
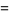 |
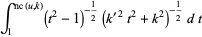 |
(39) |
 |
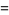 |
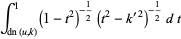 |
(40) |
 |
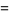 |
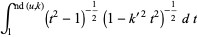 |
(41) |
 |
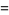 |
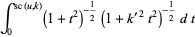 |
(42) |
 |
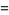 |
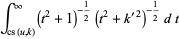 |
(43) |
 |
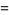 |
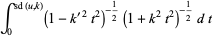 |
(44) |
 |
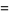 |
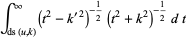 |
(45) |
 |
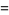 |
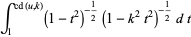 |
(46) |
 |
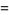 |
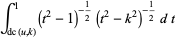 |
(47) |
(Whittaker and Watson 1990, p. 494).
Jacobi elliptic functions addition formulas include (where, for example, 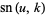 is written as
is written as 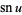 for conciseness),
for conciseness),
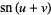 |
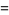 |
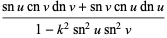 |
(48) |
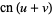 |
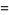 |
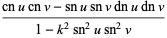 |
(49) |
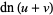 |
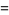 |
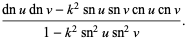 |
(50) |
Extended to integral periods,
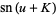 |
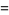 |
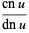 |
(51) |
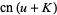 |
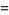 |
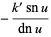 |
(52) |
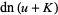 |
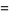 |
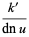 |
(53) |
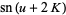 |
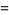 |
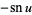 |
(54) |
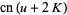 |
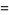 |
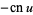 |
(55) |
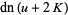 |
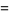 |
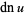 |
(56) |
For complex arguments,
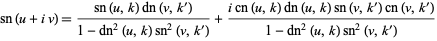 |
(57) |
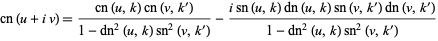 |
(58) |
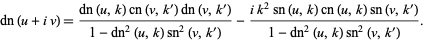 |
(59) |
Derivatives of the Jacobi elliptic functions include
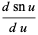 |
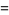 |
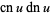 |
(60) |
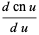 |
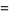 |
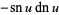 |
(61) |
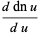 |
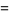 |
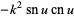 |
(62) |
(Hille 1969, p. 66; Zwillinger 1997, p. 136).
Double-period formulas involving the Jacobi elliptic functions include
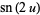 |
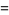 |
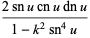 |
(63) |
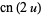 |
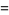 |
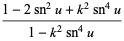 |
(64) |
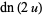 |
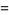 |
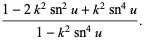 |
(65) |
Half-period formulas involving the Jacobi elliptic functions include
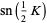 |
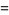 |
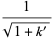 |
(66) |
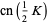 |
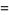 |
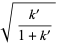 |
(67) |
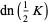 |
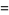 |
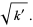 |
(68) |
Squared formulas include
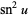 |
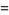 |
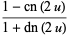 |
(69) |
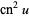 |
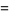 |
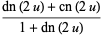 |
(70) |
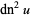 |
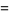 |
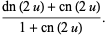 |
(71) |
Taylor series of the Jacobi elliptic functions were considered by Hermite (1863), Schett (1977), and Dumont (1981),
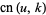 |
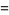 |
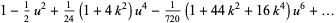 |
(72) |
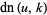 |
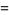 |
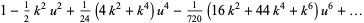 |
(73) |
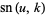 |
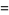 |
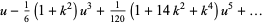 |
(74) |
(Abramowitz and Stegun 1972, eqn. 16.22).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Jacobian Elliptic Functions and Theta Functions." Ch. 16 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 567-581, 1972.
Bellman, R. E. A Brief Introduction to Theta Functions. New York: Holt, Rinehart and Winston, 1961.
Briot, C. and Bouquet, C. Théorie des fonctions elliptiques, 2nd ed. Paris: Gauthier-Villars, 1875.
Byrd, P. F. and Friedman, M. D. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed., rev. Berlin: Springer-Verlag, 1971.
Dumont, D. "Une Approach combinatoire des fonctions elliptiques de Jacobi." Adv. Math. 41, 1-39, 1981.
Hermite, C. "Remarque sur le développement de 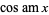 ." Comptes Rendus de l'Académie des Sciences 57, 613-618, 1863. Reprinted in J. math. pures appliq. 9, 289-295, 1864. Also reprinted in Oeuvres de Charles Hermite, Vol. 2. Paris: Gauthier-Villars, pp. 264-270, 1908.
." Comptes Rendus de l'Académie des Sciences 57, 613-618, 1863. Reprinted in J. math. pures appliq. 9, 289-295, 1864. Also reprinted in Oeuvres de Charles Hermite, Vol. 2. Paris: Gauthier-Villars, pp. 264-270, 1908.
Hille, E. Lectures on Ordinary Differential Equations. Reading, MA: Addison-Wesley, 1969.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 433, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Elliptic Integrals and Jacobi Elliptic Functions." §6.11 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 254-263, 1992.
Schett, A. "Recurrence Formula of the Taylor Series Expansion Coefficients of the Jacobi Elliptic Functions." Math. Comput. 32, 1003-1005, 1977.
Spanier, J. and Oldham, K. B. "The Jacobian Elliptic Functions." Ch. 63 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 635-652, 1987.
Tölke, F. "Jacobische elliptische Funktionen und zugehörige logarithmische Ableitungen," "Umkehrfunktionen der Jacobischen elliptischen Funktionen und elliptische Normalintegrale erster Gattung. Elliptische Amplitudenfunktionen sowie Legendresche F- und E-Funktion. Elliptische Normalintegrale zweiter Gattung. Jacobische Zeta- und Heumansche Lambda-Funktionen," and "Normalintegrale dritter Gattung. Legendresche 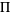 -Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 5-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 1-144, 1967.
-Funktion. Zurückführung des allgemeinen elliptischen Integrals auf Normalintegrale erster, zweiter, und dritter Gattung." Chs. 5-7 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 1-144, 1967.
Tölke, F. Praktische Funktionenlehre, vierter Band: Elliptische Integralgruppen und Jacobische elliptische Funktionen im Komplexen. Berlin: Springer-Verlag, 1967.
Trott, M. "The Mathematica Guidebooks Additional Material: ODE for Jacobi Elliptic Function sn with Respect to the Modulus." http://www.mathematicaguidebooks.org/additions.shtml#S_3_04.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, 1990.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|