


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-11-2018
Date: 27-11-2018
Date: 27-11-2018
|
The representation, beloved of engineers and physicists, of a complex number in terms of a complex exponential
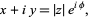 |
(1) |
where i (called j by engineers) is the imaginary number and the complex modulus and complex argument (also called phase) are
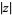 |
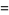 |
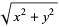 |
(2) |
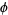 |
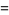 |
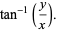 |
(3) |
Here, 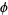 (sometimes also denoted
(sometimes also denoted 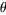 ) is called the complex argument or the phase. It corresponds to the counterclockwise angle from the positive real axis, i.e., the value of
) is called the complex argument or the phase. It corresponds to the counterclockwise angle from the positive real axis, i.e., the value of 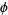 such that
such that 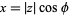 and
and 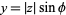 . The special kind of inverse tangent used here takes into account the quadrant in which
. The special kind of inverse tangent used here takes into account the quadrant in which 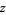 lies and is returned by the FORTRAN command ATAN2(Y,X) and the Wolfram Language function ArcTan[x, y], and is often restricted to the range
lies and is returned by the FORTRAN command ATAN2(Y,X) and the Wolfram Language function ArcTan[x, y], and is often restricted to the range 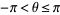 . In the degenerate case when
. In the degenerate case when 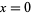 ,
,
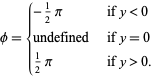 |
(4) |
It is trivially true that
![sum_(i)R[psi_i]=R[sum_(i)psi_i].](http://mathworld.wolfram.com/images/equations/Phasor/NumberedEquation3.gif) |
(5) |
Now consider a scalar function 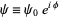 . Then
. Then
 |
 |
![[R(psi)]^2](http://mathworld.wolfram.com/images/equations/Phasor/Inline18.gif) |
(6) |
 |
 |
![[1/2(psi+psi^_)]^2](http://mathworld.wolfram.com/images/equations/Phasor/Inline21.gif) |
(7) |
 |
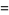 |
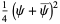 |
(8) |
 |
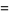 |
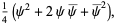 |
(9) |
where 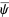 is the complex conjugate. Look at the time averages of each term,
is the complex conjugate. Look at the time averages of each term,
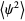 |
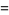 |
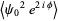 |
(10) |
 |
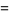 |
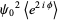 |
(11) |
 |
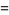 |
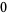 |
(12) |
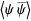 |
 |
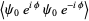 |
(13) |
 |
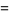 |
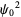 |
(14) |
 |
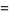 |
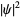 |
(15) |
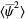 |
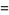 |
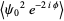 |
(16) |
 |
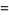 |
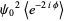 |
(17) |
 |
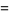 |
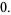 |
(18) |
Therefore,
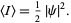 |
(19) |
Consider now two scalar functions
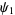 |
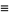 |
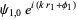 |
(20) |
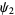 |
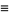 |
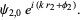 |
(21) |
Then
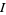 |
 |
![[R(psi_1)+R(psi_2)]^2](http://mathworld.wolfram.com/images/equations/Phasor/Inline64.gif) |
(22) |
 |
 |
![1/4[(psi_1+psi^__1)+(psi_2+psi^__2)]^2](http://mathworld.wolfram.com/images/equations/Phasor/Inline67.gif) |
(23) |
 |
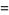 |
![1/4[(psi_1+psi^__1)^2+(psi_2+psi^__2)^2+2(psi_1psi_2+psi_1psi^__2+psi^__1psi_2+psi^__1psi^__2)]](http://mathworld.wolfram.com/images/equations/Phasor/Inline70.gif) |
(24) |
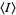 |
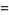 |
![1/4[2psi_1psi^__1+2psi_2psi^__2+2psi_1psi^__2+2psi^__1psi_2]](http://mathworld.wolfram.com/images/equations/Phasor/Inline73.gif) |
(25) |
 |
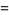 |
![1/2[psi_1(psi^__1+psi^__2)+psi_2(psi^__1+psi^__2)]](http://mathworld.wolfram.com/images/equations/Phasor/Inline76.gif) |
(26) |
 |
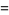 |
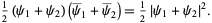 |
(27) |
In general,
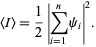 |
(28) |
REFERENCES:
Krantz, S. G. "Polar Form of a Complex Number." §1.2.4 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 8-10, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|