المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
القيمة الغذائية للثوم Garlic
2024-11-20
العيوب الفسيولوجية التي تصيب الثوم
2024-11-20
التربة المناسبة لزراعة الثوم
2024-11-20
البنجر (الشوندر) Garden Beet (من الزراعة الى الحصاد)
2024-11-20
الصحافة العسكرية ووظائفها
2024-11-19
الصحافة العسكرية
2024-11-19

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
Internet Gaming
10-10-2016
مؤشرات ضغوط العمل الإعلامي
1-9-2020
فضل القناعة عند الهادي (عليه السلام)
29-07-2015
نطاق المصلحة التي تعود على المتهم من سرعة الإجراءات
2023-03-20
THE ALGEBRA OF SETS- Expanding, factoring, and simplifying
12-1-2017
حرز لحمى الربع ـ بحث روائي
18-10-2016

Blaschke Condition  
  
402   01:15 مساءً   date: 27-11-2018
Author : Krantz, S. G
Book or Source : "The Blaschke Condition." §9.1.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser
Page and Part : ...


Read More
Vercosine
Date: 25-11-2018 450
maginary Number
Date: 24-10-2018 346
Logarithmic Capacity
Date: 1-11-2018 338

Blaschke Condition

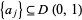If {a_j} subset= D(0,1) (with possible repetitions) satisfies

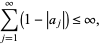sum_(j=1)^infty(1-|a_j|)<=infty,

where 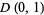D(0,1) is the unit open disk, and no 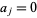a_j=0, then there is a bounded analytic function on 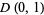D(0,1) which has zero set consisting precisely of the 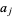a_js, counted according to their multiplicities. More specifically, the infinite product

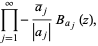product_(j=1)^infty-(a^__j)/(|a_j|)B_(a_j)(z),

where 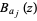B_(a_j)(z) is a Blaschke factor and 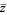z^_ is the complex conjugate, converges uniformly on compact subsets of 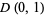D(0,1) to a bounded analytic function B(z).

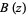REFERENCES:

Krantz, S. G. "The Blaschke Condition." §9.1.5 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 118-119, 1999.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
التاريخ / 2024-11-18

الأخبار العلمية
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
التاريخ / 2024-11-18

الساحة الاسلامية
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
التاريخ / 2024-11-19