


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-10-2018
Date: 18-11-2018
Date: 23-11-2018
|
A meromorphic function is a single-valued function that is analytic in all but possibly a discrete subset of its domain, and at those singularities it must go to infinity like a polynomial (i.e., these exceptional points must be poles and not essential singularities). A simpler definition states that a meromorphic function is a function 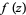 of the form
of the form
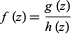 |
where 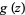 and
and 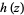 are entire functions with
are entire functions with 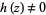 (Krantz 1999, p. 64).
(Krantz 1999, p. 64).
A meromorphic function therefore may only have finite-order, isolated poles and zeros and no essential singularities in its domain. A meromorphic function with an infinite number of poles is exemplified by 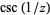 on the punctured disk
on the punctured disk 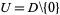 , where
, where 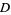 is the open unit disk.
is the open unit disk.
An equivalent definition of a meromorphic function is a complex analytic map to the Riemann sphere.
The word derives from the Greek 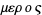 (meros), meaning "part," and
(meros), meaning "part," and 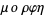 (morphe), meaning "form" or "appearance."
(morphe), meaning "form" or "appearance."
REFERENCES:
Knopp, K. "Meromorphic Functions." Ch. 2 in Theory of Functions Parts I and II, Two Volumes Bound as One, Part II. New York: Dover, pp. 34-57, 1996.
Krantz, S. G. "Meromorphic Functions and Singularities at Infinity." §4.6 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 63-68, 1999.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 382-383, 1953.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|