
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-8-2019
Date: 26-8-2019
Date: 25-5-2019
|
The first fundamental theorem of calculus states that, if 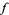 is continuous on the closed interval
is continuous on the closed interval ![[a,b]](http://mathworld.wolfram.com/images/equations/FirstFundamentalTheoremofCalculus/Inline2.gif) and
and 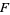 is the indefinite integral of
is the indefinite integral of 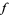 on
on ![[a,b]](http://mathworld.wolfram.com/images/equations/FirstFundamentalTheoremofCalculus/Inline5.gif) , then
, then
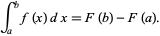 |
This result, while taught early in elementary calculus courses, is actually a very deep result connecting the purely algebraic indefinite integral and the purely analytic (or geometric) definite integral.
REFERENCES:
Anton, H. "The First Fundamental Theorem of Calculus." §5.8 Calculus: A New Horizon, 6th ed. New York: Wiley, pp. 326-335, 1999.
Apostol, T. M. "The Derivative of an Indefinite Integral. The First Fundamental Theorem of Calculus." §5.1 in Calculus, 2nd ed., Vol. 1: One-Variable Calculus, with an Introduction to Linear Algebra. Waltham, MA: Blaisdell, pp. 202-204, 1967.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|