Brent,s Method
المؤلف:
Brent, R. P
المصدر:
Ch. 3-4 in Algorithms for Minimization Without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.
الجزء والصفحة:
...
10-12-2021
1433
Brent's Method
Brent's method is a root-finding algorithm which combines root bracketing, bisection, and inverse quadratic interpolation. It is sometimes known as the van Wijngaarden-Deker-Brent method. Brent's method is implemented in the Wolfram Language as the undocumented option Method -> Brent in FindRoot[eqn, ![<span style=]()
{" src="https://mathworld.wolfram.com/images/equations/BrentsMethod/Inline1.gif" style="height:15px; width:5px" />x, x0, x1![<span style=]()
}" src="https://mathworld.wolfram.com/images/equations/BrentsMethod/Inline2.gif" style="height:15px; width:5px" />].
Brent's method uses a Lagrange interpolating polynomial of degree 2. Brent (1973) claims that this method will always converge as long as the values of the function are computable within a given region containing a root. Given three points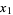 
, 
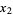, and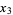 
, Brent's method fits 
as a quadratic function of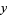 
, then uses the interpolation formula
![x=([y-f(x_1)][y-f(x_2)]x_3)/([f(x_3)-f(x_1)][f(x_3)-f(x_2)])+([y-f(x_2)][y-f(x_3)]x_1)/([f(x_1)-f(x_2)][f(x_1)-f(x_3)])+([y-f(x_3)][y-f(x_1)]x_2)/([f(x_2)-f(x_3)][f(x_2)-f(x_1)]).](https://mathworld.wolfram.com/images/equations/BrentsMethod/NumberedEquation1.gif) |
(1)
|
Subsequent root estimates are obtained by setting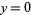 
, giving
 |
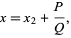(2)
|
where
with
(Press et al. 1992).
REFERENCES:
Brent, R. P. Ch. 3-4 in Algorithms for Minimization Without Derivatives. Englewood Cliffs, NJ: Prentice-Hall, 1973.
Forsythe, G. E.; Malcolm, M. A.; and Moler, C. B. §7.2 in Computer Methods for Mathematical Computations. Englewood Cliffs, NJ: Prentice-Hall, 1977.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Van Wijngaarden-Dekker-Brent Method." §9.3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 352-355, 1992.
الاكثر قراءة في التحليل العددي
اخر الاخبار
اخبار العتبة العباسية المقدسة
