


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 29-2-2016
التاريخ: 13-3-2016
التاريخ: 8-3-2016
التاريخ: 19-3-2016
|
الزوايا والتعامد في فضاء الضرب الداخلي:
سنتطرق في هذا البند إلى تعريف الزاوية بين متجهين في فضاء الضرب الداخلي وتوظيف ذلك للحصول على بعض العلاقات الاساسية بين متجهات فضاء الضرب الداخلي كالعلاقات الهندسية بين الفضاء الصفري وفضاء الأعمدة لمصفوفة ما.
تعلمنا من الفصول السابقة أنه إذا كانت v , u متجهات في R2 و θ الزاوية بينهما فإن:

مبرهنة (1-1)
(متباينة كوجي ــ شفارتز): إذا كانت u, v متجهات في فضاء الضرب الداخلي الحقيقي فإن:

البرهان:
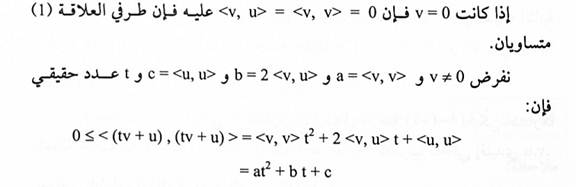
من المتباينة يتضح أن متعددة الحدود at2+bt+c اما لا تحتوي على جذور حقيقية أو جذر حقيقي متكرر. لذا فإن مميزها يحقق المتباينة.

حيث أن الصيغة الأولى حصلنا عليها بموجب مبرهنة (1-1) والصيغة الثانية حصلنا عليها من الصيغة الأول باستخدام حقيقة أن
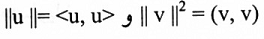
مثال(1):
لاحظ أن متباينة كوجي ــ شفارتز يمكن اعتبارها كحالة خاصة من مبرهنة (1-1) وذلك بأخذ .<v,u>كضرب داخلي إقليدي v. u.
خواص الطول والمسافة في فضاء الضرب الداخلي:
إذا كانت w, u, v متجهات في فضاء الضرب الداخلي V و k كمية ثابتة فإن:

من السهولة اثبات صحة الخواص أعلاه لذا نترك براهينها ، وللتوضيح سنبرهن الخاصية رقم 4.

ملاحظة: يتبين من خلال الخواص الثمان أن خواص المتجهات في فضاء إقليدس النوني تبقى متحققة في فضاء الضرب الداخلي.
الزاوية بين المتجهات في فضاء الضرب الداخلي:

مثال(2):
اوجد الزاوية θ المحصورة بين المتجهين v = (2,, 1,5) و u = (1, -3, 2) في R2
الحل:

تعريف (1-2):
يقال للمتجهات v و u في فضاء الضرب الداخلي بأنها متعامدة إذا تحقق الشرط الآتي:
<u,v>=0
مثال(3):

مثال(4):
لتكن p = x و q = x2 متعددتي حدود في p2 المعرف عليها الضرب الداخلي.

لذا فإن p و q متعامدتان نسبة للضرب الداخلي.
مبرهنة (1-3):
(مبرهنة فيثاغورس): إذا كانت u, v متجهات متعامدة في فضاء الضرب الداخلي، فإن:

البرهان:

مثال(5): لتكن q, p كما في المثال(4)، فإن:
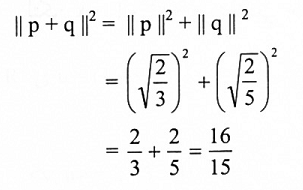
يمكن حل المثال(5): بطريقة أخرى باستخدام تعريف التكامل كالآتي:

وهي نفس النتيجة التي حصلنا عليها سابقاً.
تعريف (1-4):
لتكن U فضاء جزئي من فضاء الضرب الداخلي V. المتجه v في V يقال له عمود على U إذا كان عمودياً على كل متجه في U. مجموعة جميع المتجهات في V العمودية على U يقال لها المتممة العمودية للفضاء الجزئي U .
مبرهنة (1-5):
إذا كانت U فضاء جزئي في فضاء الضرب الداخلي V، فإن:
1. U⟘ فضاء جزئي في V.
2. المتجه الوحيد المشترك بين U, V هو المتجه الصفري.
3. المتمم العمود على U هو U [أي أن (U1)1 ] .
البرهان:
(1) نفس u, v متجهين في W1 و k كمية ثابتة، وليكن w في W، عليه فإن <u,w>=0,<v,w>=0
إذن:

مبرهنة (1-6):
لتكن A مصفوفة سعتها m x n فإن:
1. الفضاء الصفري وفضاء صفوف A هما متممان متعامدة فيR2 نسبة للضرب الداخلي الاقليدي.
2. الفضاء الصفري مصفوفة AT وفضاء أعمدة A هما متممات متعامدة في Rm نسبة للضرب الداخلي الاقليدي.
البرهان:
1. المطلوب برهانه هو إذا كان v متجه ما عمود على أي متجه في فضاء صفوف A فإن Av = 0 وبالعكس Av = 0 فإن V متعمد مع أي متجه في فضاء صفوف A لأن يعطينا أن المتممات المتعمدة لفضاء صفوف A هي الفضاء الصفري للمصفوفة A.
إذن نفرض أن v متعامد مع أي متجه في فضاء صفوف A. على وجه الخصوص نفرض v متعامد مع متجهات صفوف A، لنسميها r1 , r2, … , rn.

إذن:
عليه فإن النظام الخطي Ax = 0 يمكن كتابته بالشكل:

لهذا فإن v هو حل لهذا النظام، ومن ذلك نستنتج أن هذا الحل يقع في فضاء A الصفري.
بالعكس: نفرض أنv ينتمي لفضاء A الصفري بحيث Av = 0، لذا فإن:

ولكن إذا كان r أي متجه في فضاء صفوف A فإن r يكتب:

لهذا:

إذن v يتعامد مع كل متجه من متجهات فضاء صفوف A.
2. باستخدام برهان الجزء الاول نبرهن الجزء الثاني من خلال كون فضاء أعمدة A هو فضاء صفوف AT.
مثال(6):
أوجد المتمم العمودي على الفضاء الجزئي U في R4 المتولد من:
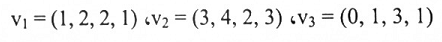

لذا فإن الفضاء الصفري للمصفوفة A، الذي هو المتمم العمودي إلى U، هو مجموعة المتجهات:

عليه فإن {(-5, 4, -2, 1)} هي أساس U1.
ملاحظة:
بإضافة الخواص الآتية:
1. المتمم العمود لفضاء A الصفري هو Rn.
2. المتمم العمودي لفضاء صفوف A هو {0}.



|
|
|
|
اكتشاف تأثير صحي مزدوج لتلوث الهواء على البالغين في منتصف العمر
|
|
|
|
|
|
|
زهور برية شائعة لتر ميم الأعصاب التالفة
|
|
|
|
|
|
المجمع العلمي يواصل دورة إعداد أساتذة قرآنيّين في النجف الأشرف
|
|
|
|
العتبة العباسية المقدسة توزع معونات غذائية في الديوانية
|
|
|
|
قسم الشؤون الفكرية يبحث سبل التعاون المشترك مع مؤسَّسة الدليل للدراسات والبحوث
|
|
|
|
قسم العلاقات العامة ينظّم برنامجًا ثقافيًّا لوفد من جامعة الكوفة
|