


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
Read More
Date: 26-4-2017
Date: 16-4-2017
Date: 25-2-2018
|
Standard Error of the Mean
The probability figures for the Gaussian distribution calculated as areas refer to the probable error for a single measurement. Thus, it is 95.4% probable that a single result from a population will lie within ±2σ of the mean m. If a series of replicate results, each containing N measurements, are taken randomly from a population of results, the mean of each set will show less and less scatter as N increases. The standard deviation of each mean is known as the standard error of the mean and is given the symbol sm. The standard error is inversely proportional to the square root of the number of data points N used to calculate the mean as given by Equation 1.1.
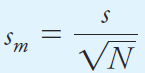 (1.1)
(1.1)
Equation 1.1 tells us that the mean of four measurements is more precise by √4 = 2 than individual measurements in the data set. For this reason, averaging results is often used to improve precision. However, the improvement to be gained by averaging is somewhat limited because of the square root dependence on N shown in Equation 1.1. For example, to increase the precision by a factor of 10 requires 100 times as many measurements. It is better, if possible, to decrease s than to keep averaging more results since sm is directly proportional to s but only inversely proportional to the square root of N. The standard deviation can sometimes be decreased by being more precise in individual operations, by changing the procedure, and by using more precise measurement tools.


|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|