


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-2-2017
Date: 8-2-2017
Date: 9-2-2017
|
Trigonometric functions of any angle
Unit circle. Counting of angles in a unit circle.
Negative and positive angles. Quarters of a unit circle.
Sine and cosine lines. Sine. Cosine. Signs of sine and
cosine in different quarters of a unit circle. Tangent
and cotangent lines. Tangent. Cotangent. Signs of
tangent and cotangent in different quarters of a unit
circle. Secant and cosecant.
To build all trigonometry, laws of which would be valid for any angles ( not only for acute angles, but also for obtuse, positive and negative angles), it is necessary to consider so called a unit circle, that is a circle with a radius, equal to 1 ( Fig.3 ).
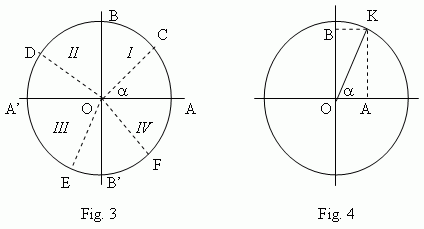
Let draw two diameters: a horizontal AA’ and a vertical BB’. We count angles off a point A (starting point). Negative angles are counted in a clockwise, positive in an opposite direction. A movable radius OC forms angle α with an immovable radius OA. It can be placed in the 1-st quarter ( COA ), in the 2-nd quarter ( DOA ), in the 3-rd quarter ( EOA ) or in the 4-th quarter ( FOA ). Considering OA and OB as positive directions and OA’ and OB’ as negative ones, we determine trigonometric functions of angles as follows.
A sine line of an angle  ( Fig.4 ) is a vertical diameter of a unit circle, a cosine line of an angle α - a horizontal diameter of a unit circle. A sine of an angle α ( Fig.4 ) is the segment OB of a sine line, that is a projection of a movable radius OK to a sine line; acosine of an angle
( Fig.4 ) is a vertical diameter of a unit circle, a cosine line of an angle α - a horizontal diameter of a unit circle. A sine of an angle α ( Fig.4 ) is the segment OB of a sine line, that is a projection of a movable radius OK to a sine line; acosine of an angle  - the segment OA of a cosine line, that is a projection of a movable radius OK to a cosine line.
- the segment OA of a cosine line, that is a projection of a movable radius OK to a cosine line.
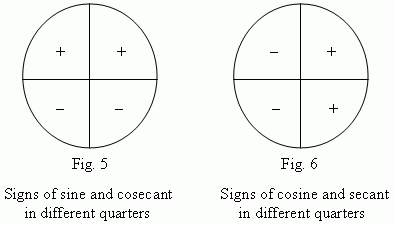
Signs of sine and cosine in different quarters of a unit circle are shown on Fig.5 and Fig.6.
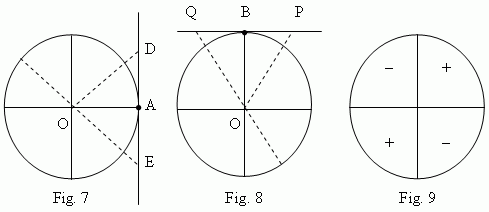
A tangent line ( Fig.7 ) is a tangent, drawn to a unit circle through the point A of a horizontal diameter.
A cotangent line ( Fig.8 ) is a tangent, drawn to a unit circle through the point B of a vertical diameter.
A tangent is a segment of a tangent line between the tangency point A and an intersection point ( D, E, etc., Fig.7 ) of a tangent line and a radius line.
A cotangent is a segment of a cotangent line between the tangency point B and an intersection point ( P, Q, etc., Fig.8 ) of a cotangent line and a radius line.
Signs of tangent and cotangent in different quarters of a unit circle see on Fig.9.
Secant and cosecant are determined as reciprocal values of cosine and sine correspondingly.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|