Died: 29 June 1924 in Washington, D.C., USA

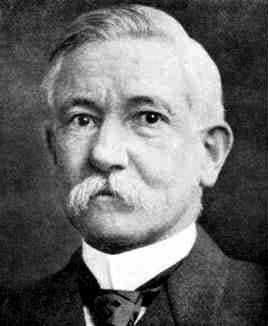
Robert Woodward's parents were Lysander Woodward and Peninah A Simpson. Lysander Woodward, a gentleman farmer, married Peninah Simpson on 11 May 1843 and they bought a large farm near the village of Rochester. In addition to running the farm, which he did using highly innovative scientific principles, Lysander held important offices in the local government of Oakland County. A leading figure in the local community, he was also president of the Oakland County Agricultural Society, and the first president of the Detroit and Bay City Railroad. Robert was brought up on his parents' farm and was quickly infected by his father's enthusiasm for applying science to agricultural methods. He attended Rochester Academy graduating in 1868. Robert wanted to continue his education at university but his father was strongly opposed to such a course for his son. However, after much persuasion by Robert, his father relented and Robert was allowed to enter the University of Michigan in 1868 to study engineering.

Woodward graduated with a C.E. from the University of Michigan in 1872. During his undergraduate years he had spent each summer doing fieldwork with the United States Lake Survey. Clearly he enjoyed his summer work for, after graduating, he spent ten years (1872-1882) working for the United States Lake Survey. His work consisted of using triangulation methods on the great lakes [3]:-

This gave him a most thorough training in primary triangulation, in latitude and longitude determinative work, in the testing of field instruments and field methods, and in the office adjustment of field observations by least-square methods.

During these years he became interested in geology, in particular becoming interested in the shape of the earth, the tides, the atmosphere and in astronomical studies. During his time with the United States Lake Survey he married Martha Gretton Bond of Detroit in that city on 1 March in 1876; they had three sons, Robert Simpson Woodward, Karl W Woodward, and William Lysander Woodward.

In 1882 he was appointed to a post with the United States Transit of Venus Commission as an assistant astronomer. The aim of the Commission was to compute an accurate value for the solar parallax and they decided to have eight observing sites, four in the United States and four abroad. Woodward went as an assistant to Asaph Hall, the discoverer of the satellites of Mars, to observe in San Antonio. The famous mathematical astronomer Simon Newcomb led the expedition to Wellington in South Africa to observe the transit from there [3]:-

... each party took a number of photographs during the transit of Venus across the sun's disk. These photographs were deposited with the Naval Observatory, where they were carefully measured, and the data of measurement were used in computations to obtain a more nearly correct value of parallax than had hitherto been possible. An immense amount of labour was put into this task, but, as a result of improvements in methods along other lines, the parallax values thus derived were superseded before the final report was completed and it was accordingly not issued.

Woodward was appointed as an astronomer to the United States Geological Survey in 1884. He was soon made a geographer rather than astronomer but after a while was promoted to chief geographer eventually becoming head of the Division of Mathematics. He published papers such as: Results of some experiments made to determine the variations in length of certain bars at the temperature of melting ice (1883), On the form and position of the sea level: With special references to its dependence on superficial masses symmetrically disposed about a normal to the Earth's surface (1888), On the Form and Position of the Sea Level (1888), Latitudes and Longitudes Of Certain Points in Missouri, Kansas, and New Mexico (1889), and Formulas and Tables to facilitate the Construction and Use of Maps (1889). As can be seen from these titles, part of Woodward's work consisted of computing latitudes and longitudes and using the data in making maps. The methods and tables he presented in his 1889 paper were of long lasting importance to the work of the Geological Survey. It is also clear from the above titles that part of his work involved the geology of the earth as a whole, particularly investigation problems concerning the sea level. His mathematical skills made him a particularly useful team member who was regularly approached by his colleagues when they ran into mathematical problems. For example the paper On the form and position of the sea level came about as a result of questions that Thomas Chrowder Chamberlin, head of the glacial division of the United States Geological Survey, had asked him concerning the area covered originally by Lake Bonneville, a prehistoric pluvial lake that covered much of North America's Great Basin region. Woodward set out to explain the difference in level of the shoreline round the edge compared to the shoreline on an island which had been in the centre of the lake [3]:-

This problem was one requiring for its solution mathematical work of the highest order and, in addition, the experience of the engineer, so to shape his formulas that they could be applied directly by the computer.

Note that 'computer' here refers to a person, not a machine. In 1889 Woodward, as Vice-President of the American Association for the Advancement of Science, gave an address on a topic which was of great current interest. The problem concerned the age of the earth which Lord Kelvin had calculated by applying his theory on the cooling of a sphere to the earth. He had come up with an age between 200 and 400 million years, and age which conflicted with evidence from geologists. Woodward had reexamined the problem and gone onto it in considerably greater depth than Lord Kelvin. His results are contained in a paper, but he gave an overview in his address to the American Association for the Advancement of Science. He discussed whether Lord Kelvin's results were likely to be correct:-

But what are the probabilities? Having been at some pains to look into this matter, I feel bound to state that, although the hypothesis appears to be the best which can be formulated at present, the odds are against its correctness. Its weak links are the unverified assumptions of an initial uniform temperature and a constant diffusivity. Very likely these are approximations, but of what order we cannot decide. Furthermore, if we accept the hypothesis, the odds appear to be against the present attainment of trustworthy numerical results, since the data for calculations, obtained mostly from observations on continental areas, are far too meager to give satisfactory average values for the entire mass of the earth. In short, this phase of the case seems to stand where it did twenty years ago, when Huxley warned us that the perfection of our mathematical mill is no guarantee of the quality of the grist, adding that as the grandest mill will not extract wheat flour from peas-cods, so pages of formulas will not get a definite result from loose data.

The argument that Lord Kelvin's results need not be correct certainly encouraged geologists. Of course, the reason that Lord Kelvin and Woodward were both wrong with their estimates of the age of the earth was only realised later when it was understood that heating of the earth occurs due to radioactivity.

In 1890 Woodward resigned from the United States Geological Survey to take up a position with the United States Coast and Geodetic Survey. The Director of the Geological Survey regretted Woodward's resignation and gave a full assessment of his contributions. He began his remarks as follows:-

... this Survey can ill afford to lose his rare ability for mathematical research. Since his first association with the Survey, in 1884, he has not only supervised the computations made in connection with the triangulation and astronomic determinations, conducted the computation of a series of tables for the use of the Topographic Branch, and given aid to geologists having occasion to read their data by mathematical methods, but he also made important additions to geologic science by discussing and advancing, on several lines, the theories of terrestrial physics.

In his new post, Woodward developed triangulation methods of surveying which were less expensive and more accurate than those employed up to that time. For example he published Geodesy: On the measurement of the base lines at Holton, Indiana and at St Albans, West Virginia 1891 and 1892 (1893) which illustrates the type of work he was undertaking at this time. Also at this time he worked on his book Smithsonian geographical tables which he published in 1894. In addition to the tables themselves, Woodward included a long preliminary discussion which contained useful formulas and a section on the theory of errors.

In 1893 Woodward was appointed Professor of Mechanics at Columbia University. On 26 November 1894 he addressed the New York Academy of Sciences which the lecture An historical survey of the science of mechanics. He was one of the two editors of Higher mathematics: a textbook for classical and engineering colleges (1896) to which he contributed an important chapter entitled Probability and theory of errors. From 1899 until 1904 he was Professor of Mechanics and Mathematical Physics at Columbia. He spent 12 years at Columbia during which [2]:-

... he was remarkably successful both as teacher and as administrator. He had a most attractive, genial, and lovable personality, and his advice was being so constantly sought by students and members of the faculty, that he found it very difficult to pursue mathematical work to which he had looked forward.

During his time in New York, Woodward was closely associated with the American Mathematical Society. He was vice-president of the Society from 1897 to 1898 and president from 1899 to 1900. Among his publications during his time at Columbia University we mention: The century's progress in applied mathematics: Presidential address to the American Mathematical Society (1900), Mathematical Theories of the Earth (1900), Observation and experiment: New York Academy of Sciences (1901), Measurement and calculation: Presidential address to the New York Academy of Sciences (1902), The Unity of Physical Science (1904), and Academic ideals: Address at the opening of Columbia University (1904). However, he also published several papers in the Bulletin of the American Mathematical Society such as: On the cubic equation defining the Laplacian envelope of the earth's atmosphere (1897), On the integration of a system of simultaneous linear differential equations (1897), On the differential equation defining the Laplacian distribution of density, pressure, and acceleration of gravity in the earth (1898), On the mutual gravitational attraction of two bodies whose mass distributions are symmetrical with respect to the same axis (1898), and An elementary method of integrating certain linear differential equations (1900).

In 1904 Woodward left New York to take up the post of president of the newly formed Carnegie Institute of Washington which had been set up with ten million dollars gifted by Andrew Carnegie to promote study and research. He became the second president of the Institute, taking up his post on 13 December 1904. Raymond Archibald [2] writes:-

At this critical period, his mature judgement and experience, his clarity of vision, common sense, enthusiasm, and geniality, led ... to the establishment on a firm foundation...

After examining the science produced from the award of small grants by the Institute, he concluded that the best way to further science was for the Institute to concentrate on awarding large grants to fund major projects mainly by investigators employed by the Institution. One reason for moving support away from colleges and universities was his realisation that when the Institute made a grant to such an outside institution, the researchers in that institution lost grant income from internal sources. His policy was adopted and led to major advances by the Geophysical Laboratory and the Mount Wilson Observatory. The book [1] contains a wealth of information about the conflicts Woodward had to overcome in his leadership of the Carnegie Institute. When World War I broke out in Europe, Woodward was greatly disturbed. As soon as the United States entered the war, Woodward offered the services of the Carnegie Institute for war work [2]:-

The war work of the Carnegie Institution covered many fields of activity, from the manufacture of optical glass to military intelligence work, and to it all Dr Woodward offered the most effective support. He himself was a member of the Naval Consulting Board, as one of the two representatives from the American Mathematical Society to the board.

Woodward received many honours in addition to those associated with the American Mathematical Society quoted above. He was elected President of the New York Academy of Sciences (1900-1902), the Philosophical Society of Washington (1910), the Literary Society of Washington (1913-1914), and the Washington Academy of Sciences (1915). He was elected to the National Academy of Sciences in 1896 and served the Academy on its Council and as Chairman of many of its committees. He was awarded honorary degrees by the University of Michigan (1892 and 1912), the University of Wisconsin (1904), the University of Pennsylvania (1905), Columbia, University (1905), and Johns Hopkins University (1915). He was an editor of Science from 1884 to 1924, and of the Annals of Mathematics from 1888 to 1889.

As to Woodward's character, we quote from [2]:-

Woodward possessed a simplicity and open friendliness of manner and character that endeared him to young and old alike. It was a privilege to know him, to feel his radiant enthusiasm, and to be uplifted by his hopeful outlook on this world and its many problems.

Books:

1. R E Kohler, Partners in Science: Foundations and Natural Scientists, 1900-1945 (University of Chicago Press, Chicago, 1991).

Articles:

1. R C Archibald, Robert Simpson Woodward, in A semicentennial history of the American Mathematical Society 1888-1938 (New York, 1980), 139-144.
2. Obituary : Dr R S Woodward, Nature 114 (1924), 510.
3. Robert Simpson Woodward, Science 61 (1589) (1925), 603-604.
4. Sees science rise from the ashes of war, The New York Times (19 March 1922).
5. K W Woodward, Robert Simpson Woodward, Science 64 (1652) (1926), 207.
6. F E Wright, Biographical Memoir of Robert Simpson Woodward, National Academy Biographical Memoirs 19 (1937), 1-24.
7. F E Wright, Memorial of Robert Simpson Woodward, Bull. Geological Soc. Amer. 37 (1) (1926), 115-134.