


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 16-9-2020
Date: 24-5-2016
Date: 1-1-2017
|
Ideal Gases
One of the most fundamental properties of any macroscopic system is the so-called equation of state. This is the equation that specifies the exact relation between pressure p, volume V , and temperature T for a substance. The equation of state for a gas is very different to the equation of state of a liquid. Actually there is a giant accelerator, called the Relativistic Heavy Ion Collider (RHIC) currently under construction at Brookhaven National Laboratory on Long Island. This accelerator will collide heavy nuclei into each other at extremely high energies. One of the main aims is to determine the nuclear matter equation of state at very high temperatures and densities, simulating the early universe. Now it turns out that most gases obey a simple equation of state called the ideal gas law
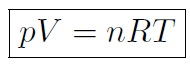
where p is the pressure, V is the volume, T is the temperature (in oK), n is the number of moles of the gas and R is the so called gas constant with the value
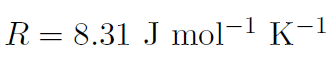
Recall that the number of molecules is given by N = nNA where n is the number of moles. Thus 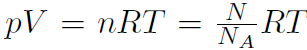 and define Boltzmann's constant
and define Boltzmann's constant
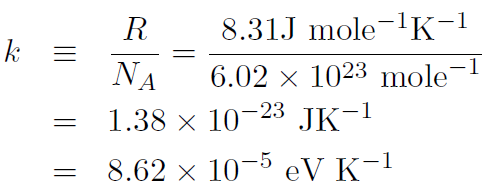
where an electron volt is defined as
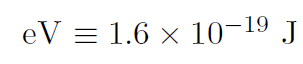
Thus the ideal gas law is also often written as
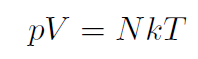
where N is the total number of molecules.
The ideal gas law embodies exactly the properties we expect of a gas:
1) If the volume V is held constant, then the pressure p increases as temperature T increases.
2) If the pressure p is held constant, then as T increases, p increases.
3) If the temperature T is held constant, then as p increases, V decreases.
Work Done by an Ideal Gas
The equation of state can be represented on a graph of pressure vs. volume, often called a pV diagram. Remember an equation of state is an equation relating the three variables p, V , T. A pV diagram takes care of two variables. The third variable T represents different lines on the pV diagram. These difference lines are called isotherms (meaning same temperature). For fixed T (say 310 K) the pressure is inversely proportional to volume as specified in the ideal gas law. Would look different for an equation of state different from the ideal gas law.
Example What is the work done by any gas (ideal or not) at constant volume (isometric) ?
Solution If Vi = Vf then
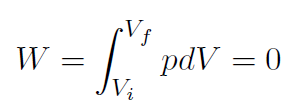
which is obvious when we think of the piston in the previous chapter. If the volume does not change then the piston doesn't move and the work is zero.
Example Derive a formula for the work done by any gas (ideal or not) which expands isobarically (i.e. at constant pressure).
Solution If p is a constant it can be taken outside the integral, giving
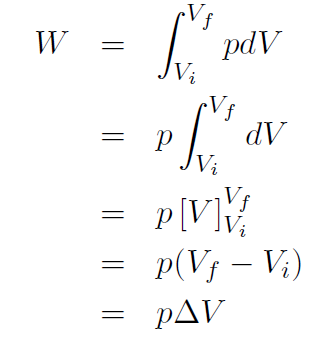
Example Derive a formula for the work done by a gas when it expands isothermally (i.e. at constant temperature).
Solution The work done by an expanding gas is given by
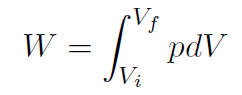
But this time the pressure changes. For an ideal gas we have 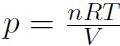 giving
giving
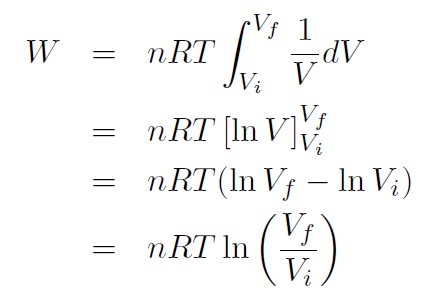



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|