


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-10-2016
Date: 8-10-2016
Date: 9-10-2016
|
For this section, we will again take A to be the cube [−1, 1] m in Rm.
DEFINITION. A control α(.) ∈ A is called bang-bang if for each time t ≥ 0 and each index i = 1, . . . ,m, we have |αi(t)| = 1, where
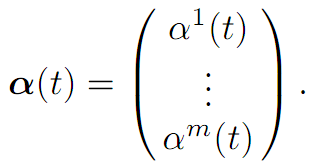
THEOREM 1.1 (BANG-BANG PRINCIPLE). Let t > 0 and suppose x0 ∈C(t), for the system
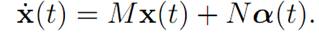
Then there exists a bang-bang control α(.) which steers x0 to 0 at time t.
To prove the theorem we need some tools from functional analysis, among hem the Krein–Milman Theorem, expressing the geometric fact that every bounded onvex set has an extreme point.
1.1 SOME FUNCTIONAL ANALYSIS. We will study the “geometry” of certain infinite dimensional spaces of functions.
NOTATION:
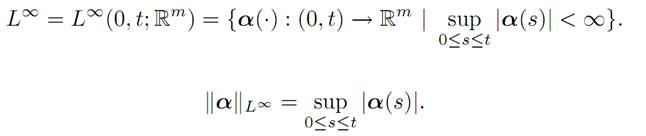
DEFINITION. Let αn ∈ L∞ for n = 1, . . . and α ∈ L∞. We say αn converges to α in the weak* sense, written
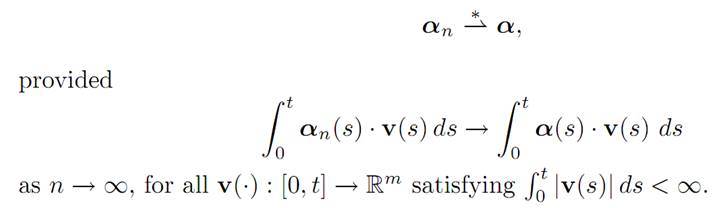
We will need the following useful weak* compactness theorem for L∞:
ALAOGLU’S THEOREM. Let αn ∈ A, n = 1, . . . . Then there exists a subsequence αnk and α ∈ A, such that
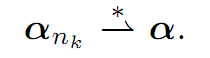
DEFINITIONS. (i) The set K is convex if for all x, xˆ ∈ K and all real numbers 0 ≤ λ ≤ 1,
λx + (1 − λ) xˆ ∈ K.
(ii) A point z ∈ K is called extreme provided there do not exist points x, xˆ ∈ K and 0 < λ < 1 such that
z = λx + (1 − λ) xˆ.
KREIN-MILMAN THEOREM. Let K be a convex, nonempty subset of L∞, which is compact in the weak ∗ topology.
Then K has at least one extreme point.
1.2 APPLICATION TO BANG-BANG CONTROLS.
The foregoing abstract theory will be useful for us in the following setting. We will take K to be the set of controls which steer x0 to 0 at time t, prove it satisfies the hypotheses of Krein–Milman Theorem and finally show that an extreme point is a bang-bang control.
So consider again the linear dynamics
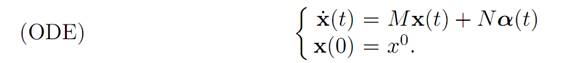
Take x0 ∈ C(t) and write
K = {α(.) ∈ A |α(.) steers x0 to 0 at time t}.
LEMMA 1.3 (GEOMETRY OF SET OF CONTROLS). The collection K of admissible controls satisfies the hypotheses of the Krein–Milman Theorem.
Proof. Since x0 ∈ C(t), we see that K = ∅.
Next we show that K is convex. For this, recall that α(.) ∈ K if and only if
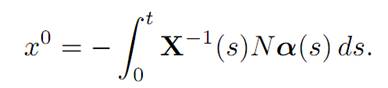
Now take also αˆ ∈ K and 0 ≤ λ ≤ 1. Then
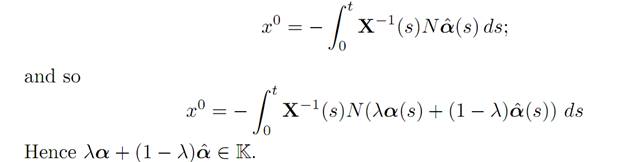
Lastly, we confirm the compactness. Let αn ∈ K for n = 1, . . . . According to Alaoglu’s Theorem there exist nk → ∞ and α ∈ A such that αnk∗⇀ α. We need
to show that α ∈ K.
Now αnk ∈ K implies
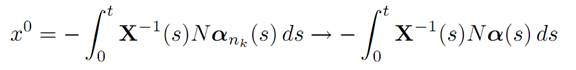
by definition of weak-* convergence. Hence α ∈ K.
We can now apply the Krein–Milman Theorem to deduce that there exists an extreme point α∗ ∈ K. What is interesting is that such an extreme point corresponds to a bang-bang control.
THEOREM 1.4 (EXTREMALITY AND BANG-BANG PRINCIPLE). The control α∗(.) is bang-bang.
Proof. 1. We must show that for almost all times 0 ≤ s ≤ t and for eachi = 1, . . . ,m, we have
|αi∗ (s)| = 1.
Suppose not. Then there exists an index i ∈ {1, . . . ,m} and a subset E ⊂ [0, t] of positive measure such that |αi∗(s)| < 1 for s ∈ E. In fact, there exist a number ε > 0 and a subset F ⊆ E such that
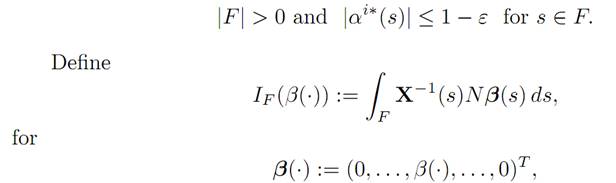
the function β in the ith slot. Choose any real-valued function β(.) ≡ 0, such that IF (β(.)) = 0
and |β(.)| ≤ 1. Define
α1(.) := α∗(.) + εβ(.)
α2(.) := α∗(.) − εβ(.),
where we redefine β to be zero off the set F
2. We claim that
α1(.),α2(.) ∈ K.
To see this, observe that
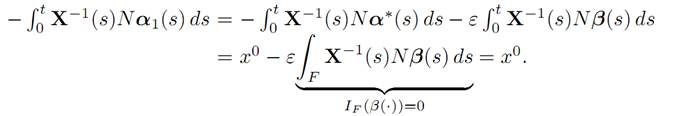
Note also α1(.) ∈ A. Indeed,
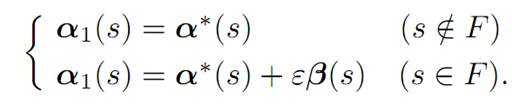
But on the set F, we have |α∗i (s)| ≤ 1 − ε, and therefore
|α1(s)| ≤ |α∗ (s)| + ε|β(s)| ≤ 1 − ε + ε = 1.
Similar considerations apply for α2. Hence α1,α2 ∈ K, as claimed above.
3. Finally, observe that
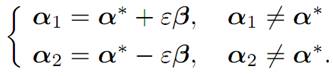
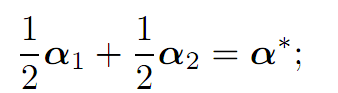
and this is a contradiction, since α∗ is an extreme point of K.
References
[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.
[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.
[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.
[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.
[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.
[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.
[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.
[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.
[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.
[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).
[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.
[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.
[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.
[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.
[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.
[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.
[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.
[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.
[T] William J. Terrell, Some fundamental control theory I: Controllability, observability, and duality, American Math Monthly 106 (1999), 705–719.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|