EXAMPLE 1: ROCKET RAILROAD CAR. We recall this example, introduced in §1.2. We have
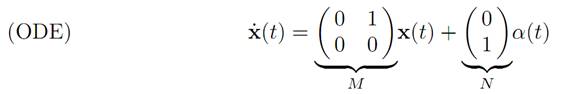
For
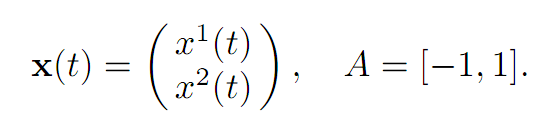
According to the Pontryagin Maximum Principle, there exists h≠0 such that
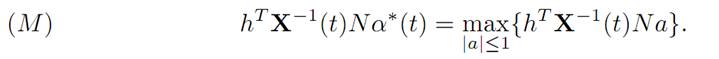
We will extract the interesting fact that an optimal control α∗ switches at most one time.
We must compute etM. To do so, we observe
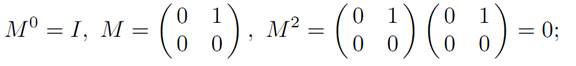
and therefore Mk = 0 for all k ≥ 2. Consequently,
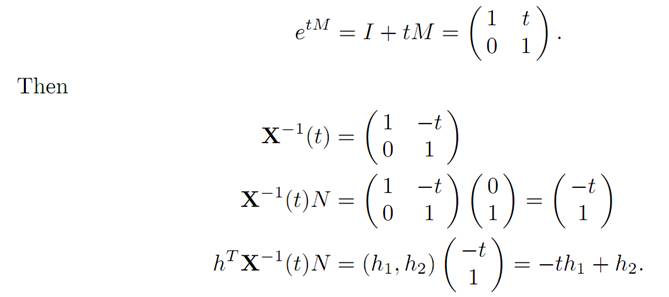
The Maximum Principle asserts
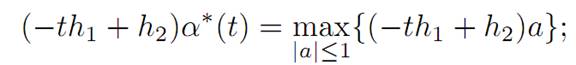
and this implies that
α∗ (t) = sgn(−th1 + h2)
for the sign function
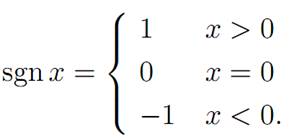
Therefore the optimal control α∗ switches at most once; and if h1 = 0, then α∗ is constant.
Since the optimal control switches at most once, then the control we constructed by a geometric method in §1.3 must have been optimal.
EXAMPLE 2: CONTROL OF A VIBRATING SPRING. Consider next the simple dynamics
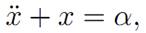
where we interpret the control as an exterior force acting on an oscillating weight (of unit mass) hanging from a spring. Our goal is to design an optimal exterior forcing α∗(.) that brings the motion to a stop in minimum time.
We have n = 2, m = 1. The individual dynamical equations read:
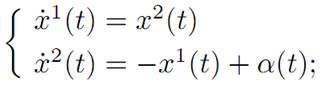
which in vector notation become
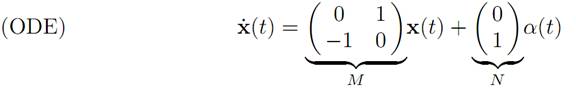
for |α(t)| ≤ 1. That is, A = [−1, 1].
Using the maximum principle. We employ the Pontryagin Maximum Principle, which asserts that there exists h ≠ 0 such that
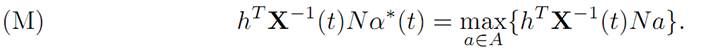
To extract useful information from (M) we must compute X(.). To do so, we observe that the matrix M is skew symmetric, and thus
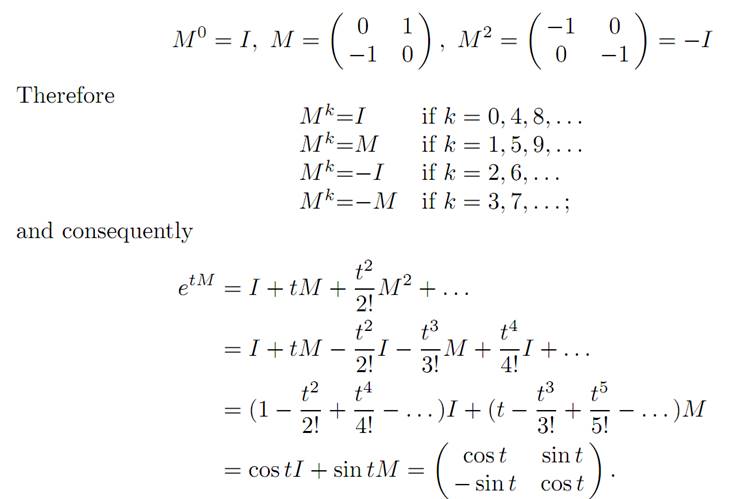
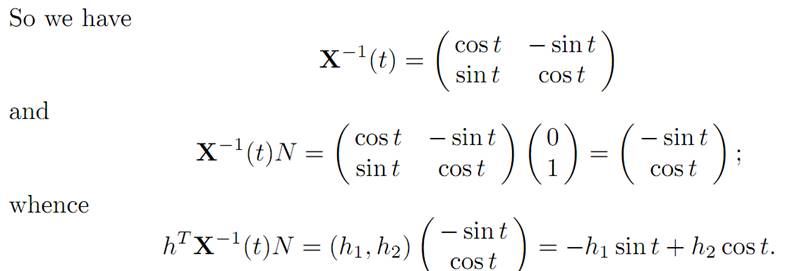
According to condition (M), for each time t we have
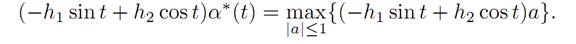
Therefore
α∗(t) = sgn(−h1 sin t + h2 cos t).
Finding the optimal control. To simplify further, we may assume h21+h22 =1. Recall the trig identity sin(x + y) = sin x cos y + cos x sin y, and choose δ such that
−h1 = cos δ, h2 = sin δ. Then
α∗ (t) = sgn(cos δ sin t + sin δ cos t) = sgn(sin(t + δ)).
We deduce therefore that α∗ switches from +1 to −1, and vice versa, every π units of time.
Geometric interpretation. Next, we figure out the geometric consequences.
When α ≡ 1, our (ODE) becomes
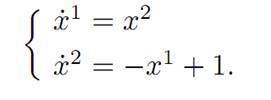
In this case, we can calculate that
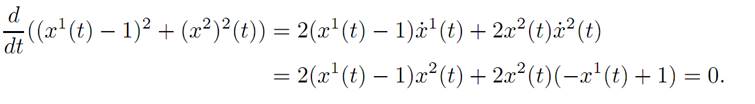
Consequently, the motion satisfies (x1(t) − 1)2 + (x2)2(t) ≡ r21, for some radius r1, and therefore the trajectory lies on a circle with center (1, 0), as illustrated.
If α ≡ −1, then (ODE) instead becomes
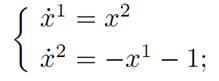
in which case
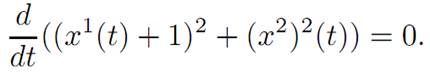
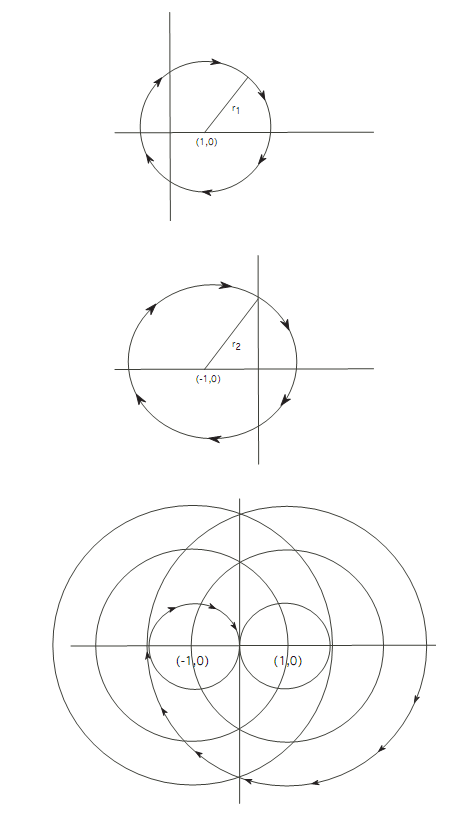
Thus (x1(t)+1)2 +(x2)2(t) = r22 for some radius r2, and the motion lies on a circle with center (−1, 0).
In summary, to get to the origin we must switch our control α(.) back and forth between the values ±1, causing the trajectory to switch between lying on circles centered at (±1, 0). The switches occur each π units of time.
References
[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.
[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.
[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.
[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.
[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.
[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.
[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.
[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.
[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.
[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).
[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.
[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.
[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.
[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.
[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.
[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.
[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.
[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.
[T] William J. Terrell, Some fundamental control theory I: Controllability, observability, and duality, American Math Monthly 106 (1999), 705–719.
 الاكثر قراءة في نظرية التحكم
الاكثر قراءة في نظرية التحكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


