Isothermal Compression and Adiabatic Expansion of Ideal Gas

An ideal gas is compressed at constant temperature τ from volume V₁ to volume V₂ (see Figure 1.1).

a) Find the work done on the gas and the heat absorbed by the gas.

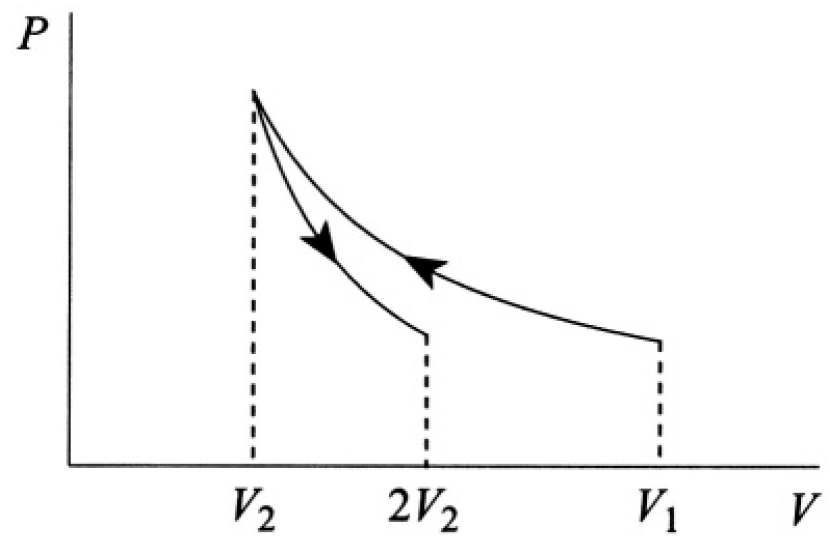
Figure 1.1

b) The gas now expands adiabatically to volume 2V₂. What is the final temperature T_f (derive this result from first principles)?

c) Estimate T_f for T_i = 300 K for air.

SOLUTION

We can a) calculate the work as an integral, using the ideal gas law:

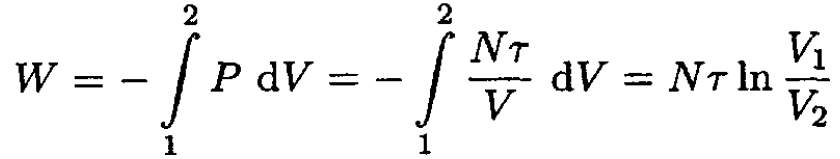(1)

where τ is, as usual, the absolute temperature. Graphically, it is simply the area under the curve (see Figure 1.2). Alternatively, we can say that the work done is equal to the change of free energy F of the system:

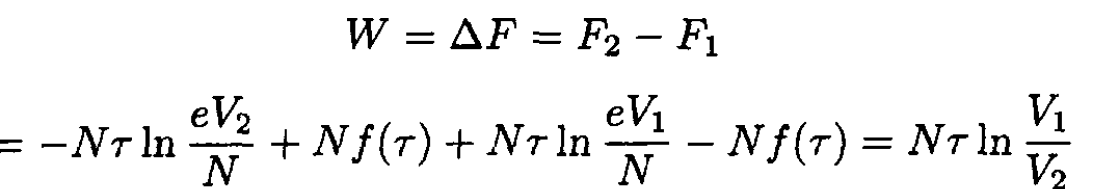(2)

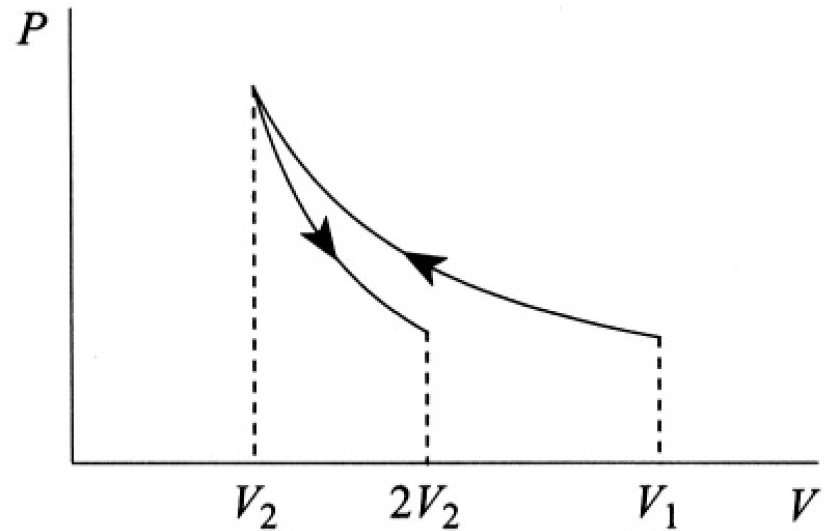
Figure 1.2

The total energy ε of the ideal gas depends only on the temperature, which is constant, so the heat absorbed by the gas is

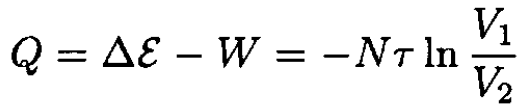(3)

i.e., heat is rejected from the gas into the reservoir. Alternatively, since δQ = τ dS,

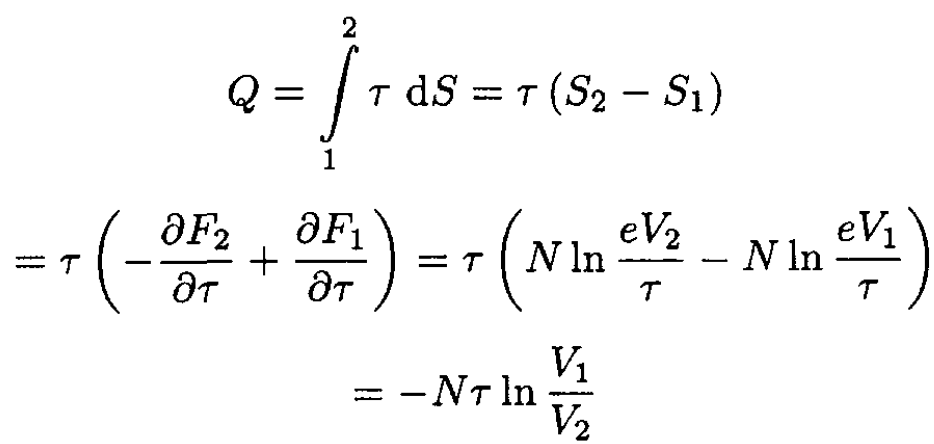(4)

the same result as in (3).

b) For an adiabatic expansion the entropy is conserved, so

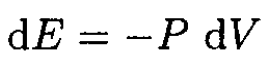(5)

On the other hand,

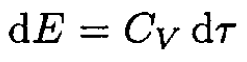(6)

where C_V is the specific heat for an ideal gas at constant volume. From (5) and (6), and using the ideal gas law, we obtain

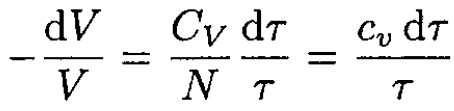(7)

where C_V/N ≡ c_v, the specific heat per one molecule. Integrating (7) yields

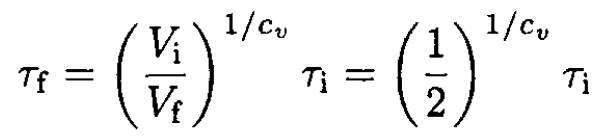(8)

c) For air we may take c_v = 5/2 (in regular units, c_v  = 5k_B/2, it is mostly diatomic). Therefore,