


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 13-7-2016
Date: 15-3-2021
Date: 23-8-2016
|
Potential of Charged Rod
A thin non-conducting rod of length L carries a uniformly distributed charge Q and is oriented as shown in Figure 1.1.
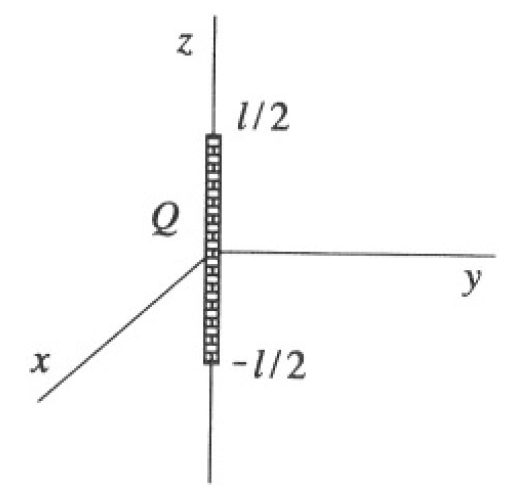
Figure 1.1
a) Find the potential ϕ due to the charged rod for any point on the x-axis with z > L/2.
b) Find ϕ(r, θ, φ) for all |r| > L/2 where r, θ, φ are the usual spherical coordinates.
Hint: The general solution to Laplace’s equation in spherical coordinates is
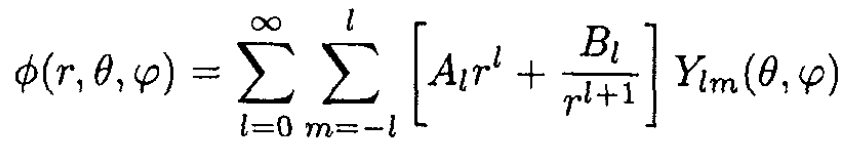 (i)
(i)
SOLUTION
a) The potential along the z-axis may be computed by integrating along the rod:
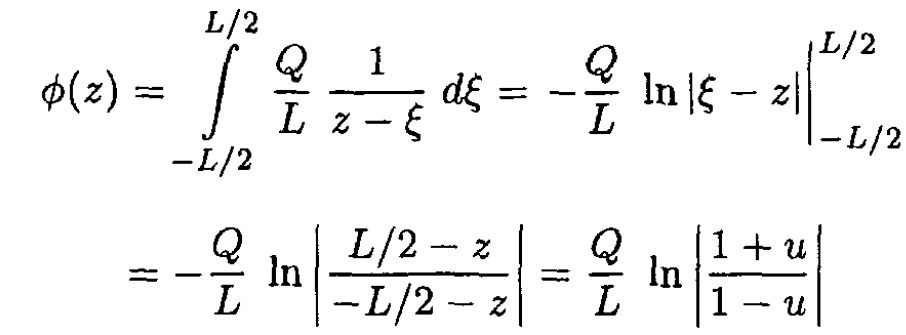 (1)
(1)
where u ≡ L/2z.
b) Since the problem has azimuthal symmetry, we may use the Legendre polynomials Pl (cosθ) and rewrite the expansion in (i) (see Figure 1.2)
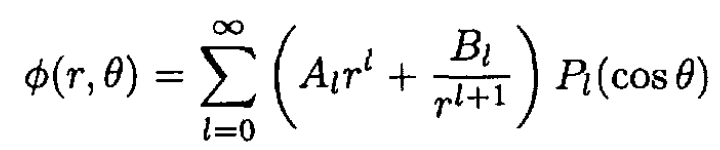
Since we consider r > L/2, all the Al are zero, and
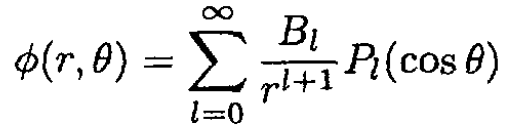 (2)
(2)
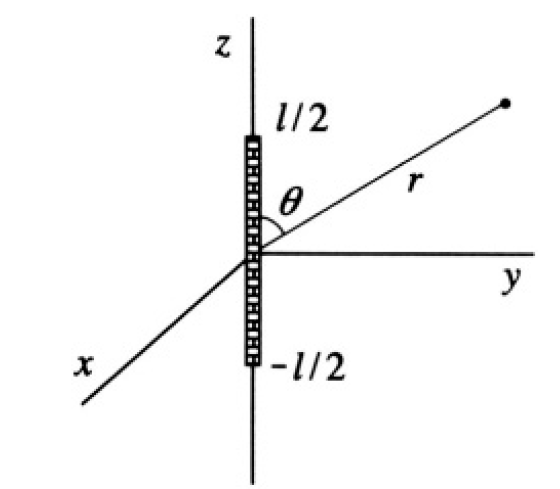
Figure 1.2
We wish to equate (2) along the with z-axis (1) where Pl(1) = 1 for all l. We must rewrite ln|(1+u)/(1-u)| as a sum. Now,
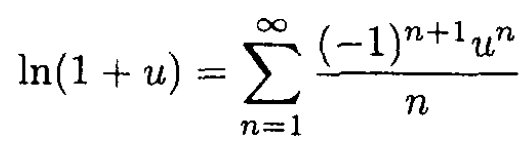
So
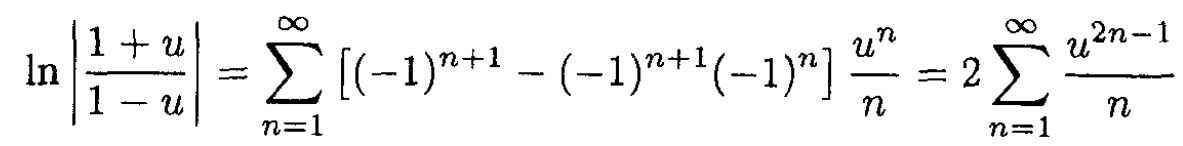 (3)
(3)
Rewriting (1) using (3), we find
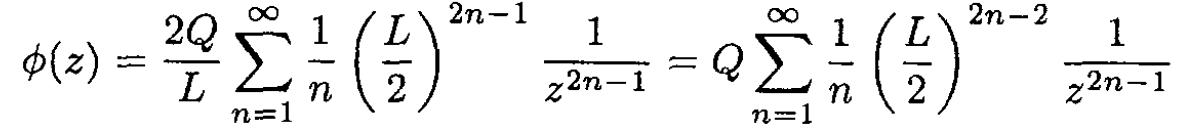
Replacing n by l + 1,
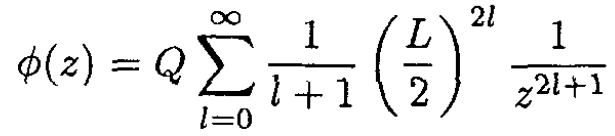 (4)
(4)
Using (2) and (4), we have
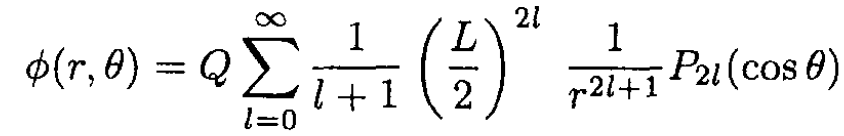



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|