Coaxial Cable and Surface Charge

A very long coaxial cable consists of an inner cylinder of radius a and isotropic conductivity σ and a concentric outer cylinder of radius b. The outer shell has infinite conductivity. The space between the cylinders is empty. A uniform, constant current density J, directed along the axial coordinate z, is maintained in the inner cylinder. Return current flows

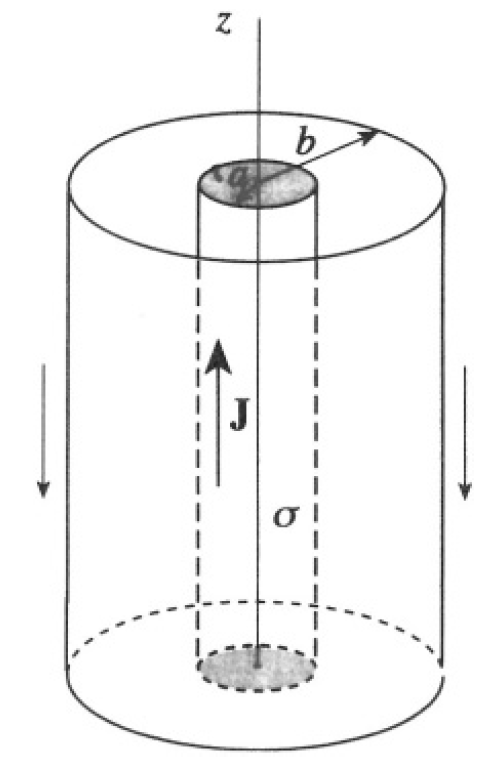
Figure 1.1

uniformly in the outer shell (see Figure 1.1). Compute the surface charge density on the inner cylinder as a function of the axial coordinate z, with the origin z = 0 chosen to be the plane halfway between the two ends of the cable.

SOLUTION

Write down Laplace’s equation in the region between the cylinders in cylindrical coordinates:

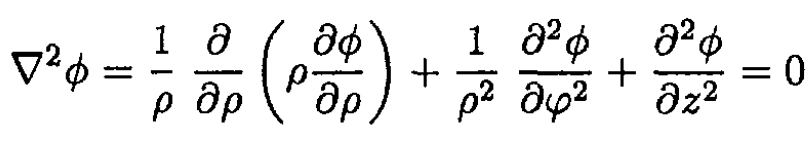
By cylindrical symmetry, ϕ does not depend on φ (see Figure 1.2), so

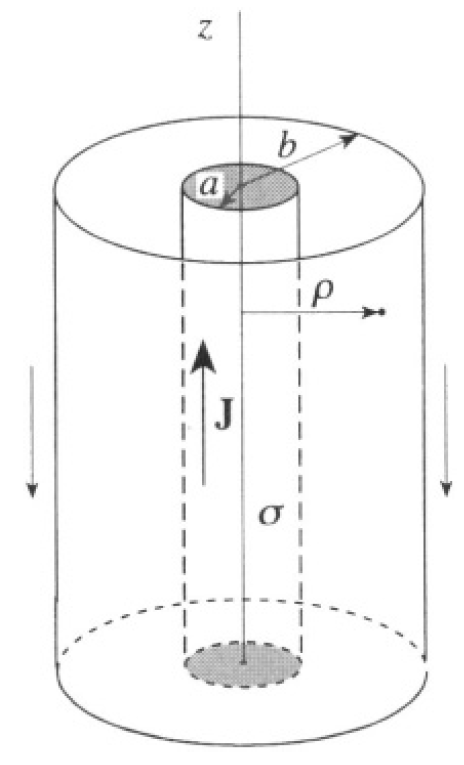
Figure 1.2

Laplace’s equation reduces to

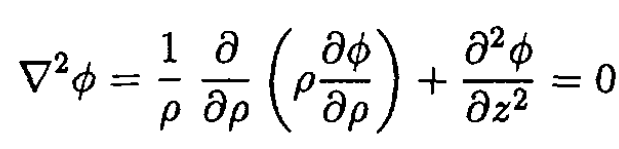(1)

As usual, we look for a solution in the form

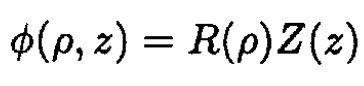
and (1) becomes

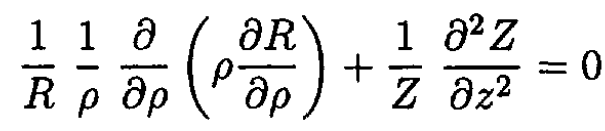(2)

From (2), we have

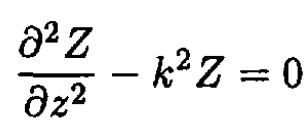(3)

where k is a constant. By translational symmetry along the z-axis

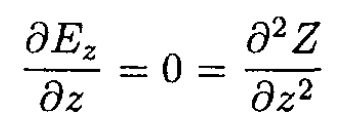
so k = 0, and

where α and β are constants. The radial part then becomes

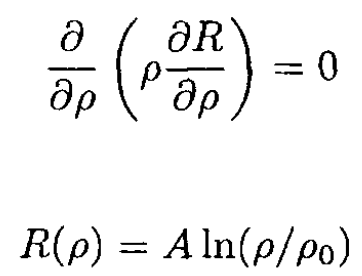(4)

So

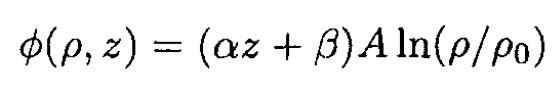(5)

Imposing the boundary condition that ϕ (ρ, 0) = 0 leads to β = 0, and we have

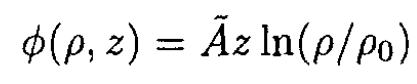(6)

where à is a constant (à = αA). We may write the potential differences along the cable as

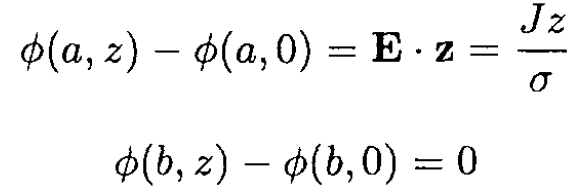(7)

where we used J = σE, the uniformity of the current density J and isotropic electrical conductivity. We now have

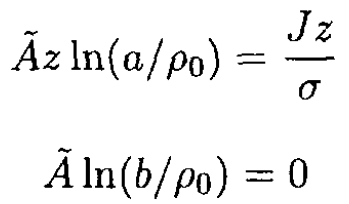(8)

From (8), we find

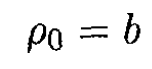(9)

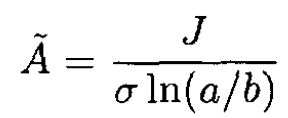(10)

For ρ < a, the potential is the same as on the surface, and from (7)and (9)

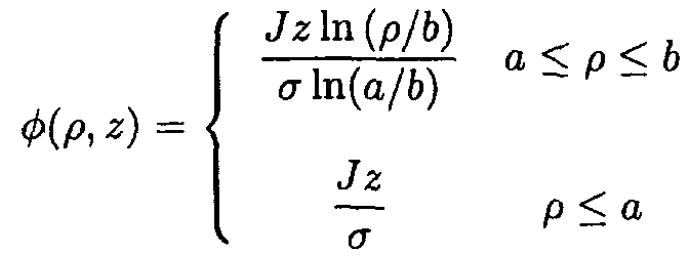
The surface charge density is

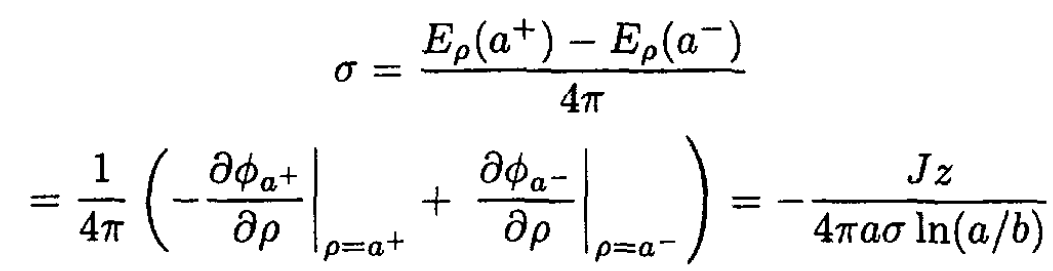
where a⁺ and a^- correspond to the points outside and inside the inner cylinder, respectively.