


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 29-8-2016
Date: 11-8-2016
Date: 2-8-2016
|
Yukawa Force Orbit
A particle of mass m moves in a circle of radius R under the influence of a central attractive force
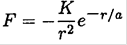
a) Determine the conditions on the constant α such that the circular motion will be stable.
b) Compute the frequency of small radial oscillations about this circular motion.
SOLUTION
The motion can be investigated in terms of the effective potential
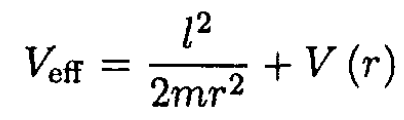 (1)
(1)
where l is the angular momentum of the particle about the origin and
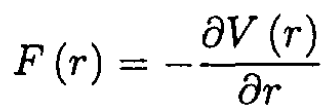
The conditions for a stable orbit are
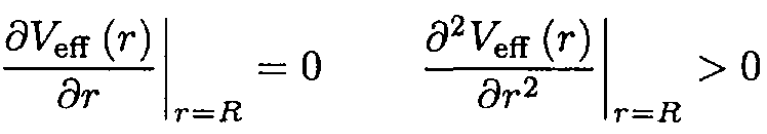 (2)
(2)
where r = R is an equilibrium point for the particle in this now one dimensional problem. The requirement on the second derivative implies that the effective potential is a minimum, i.e., the orbit is stable to small perturbations. Substituting (1) into (S2), we obtain
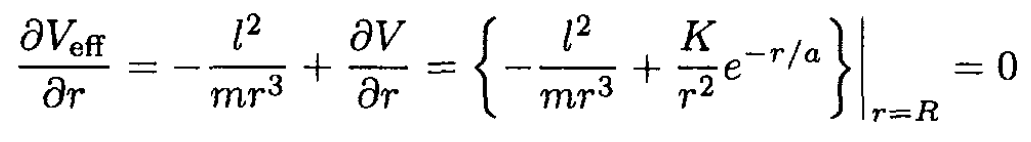 (3)
(3)
The second condition of (2) gives
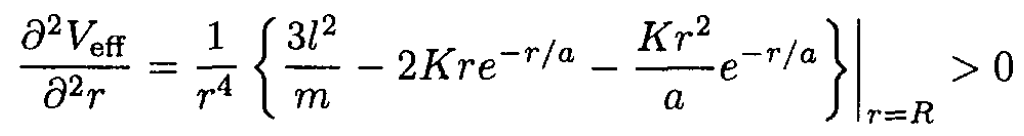 (4)
(4)
(3) gives
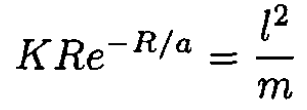
which, substituted into (4), yields
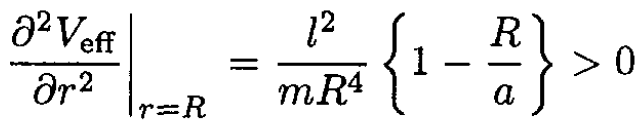 (5)
(5)
which implies that, for stability, a > R.
b) The equation for small radial oscillations with ζ = r - R is
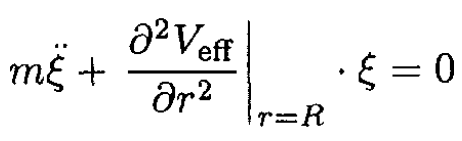 (6)
(6)
The angular frequency for small oscillations given by (5) and (6) is found from
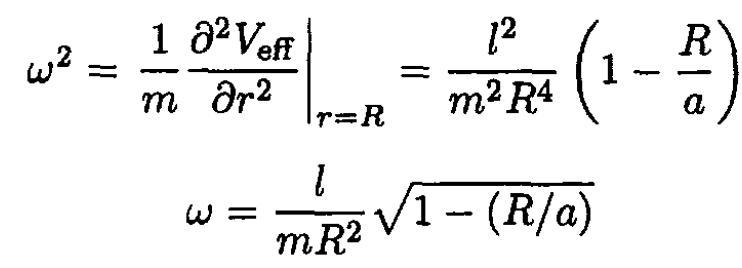



|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|