REQUIRED   PUMP   POWER   AND   EFFICIENCY

     At this stage of the analysis we can model a simple (ideal) laser system mathematically and calculate key parameters for operation, including the minimum pump power required to generate an inversion (and hence a gain) sufficient to overcome losses in the laser system. We begin by expressing the minimum pump energy that must be delivered to the system:

 (1.1)

where V is the active volume of the amplifier and hv_mp is the photon energy required at the ULL. The photon energy in this case is the energy of the ULL above ground state; in other words, the energy that a photon at the ULL must possess to emit a lasing photon and decay further to ground state. In a three-level laser this is equal to the photon energy of the lasing transition itself, but in a four-level laser this energy is equal to the energy of the lasing transition plus the energy of the LLL above ground.

      The rate dN_ULL/dt in the equation is the rate at which energy decays from the pump level to the upper lasing level and so represents the energy flowing into the ULL from the pump level above. A substitution for this rate may be determined by solving the equation for decay of the level, which expresses the population of the level at any time t as

 (1.2)

where N_ULL(0) is the population of the ULL at time t =0 and τ is the spontaneous lifetime of the level. This is the exponential decay rate of the upper lasing level as a function of time. With no external input of energy, the level decays in population to 37% of its initial value within the time period of one spontaneous lifetime (this is, in fact, the definition of spontaneous lifetime). Taking the differential of the equation with respect to time yields an answer of

 (1.3)

which describes the first term of our equation. Further substitution may now be made by realizing that in a four-level laser, , where ΔN is the population inversion of the laser (which also represents the number of coherent photons in the laser itself since we assume that in an ideal laser each excited atom produces one photon of coherent light). This substitution assumes a negligible population of atoms at the LLL since the decay rate from the LLL to ground would be much faster than that of the lasing transition in an ideal laser. For a three-level laser the population of the LLL is far from negligible (since the LLL is the ground state itself ), so the number of coherent photons is equal to the population difference between the two lasing transition levels (), so  (where N_ULL = N₂ for a three-level laser).

     Consider now the threshold population inversion as stated. Knowing the reflectivities of both cavity mirrors as well as loss in the lasing medium, we may calculate the threshold population inversion and further equate this to N₂ using the approximation stated. Furthermore, by determining the spontaneous lifetime of the lasing species, we may solve the required rate of transitions from the ULL to the LLL (i.e., dN_ULL/dt). Finally, computation of the volume and photon energy of the system allows solution of the minimum required pump power.

Example 1.1 Minimum Required Pump Power Consider the pump power required for an optically pumped Nd :YAG laser with a rod 4 mm in diameter and 5 cm in length. The material has a transition cross section of 6.5 × 10^-19 cm² and a spontaneous lifetime of 1.2 ms. The laser cavity has one mirror 100% reflecting and the OC 90% reflecting. Loss in YAG is approximately 0.01 m^-1. The rate of transitions required is dN_ULL/dt = -1/τ_NULL, for which we substitute N_ULL = ΔN_th as follows:

So to oscillate a laser with the losses specified requires 2.73 × 10²¹ transitions per second per cubic centimeter of lasing medium. We may also easily calculate volume of the rod as 0.628 cm³. The final parameter required is the energy of the photon required at the ULL. We know that the YAG laser has a wavelength of 1064 nm, which corresponds to a photon energy of 1.87 × 10^-19 J, but we must add this energy to that of the LLL above ground. A good physics reference lists the energy of the LLL as 2.4 × 10^-20 J above the ground state of the Nd3‏ ion, so that hv_mp is  2.11 × 10^-19 J. This may also have been found be calculating the energy of the 946 nm transition in YAG and adding the energy of the LLL above ground for that transition (which, as we had seen in an earlier example, is only 0.1 eV). The pump energy required is then found using equation (1.1) to be

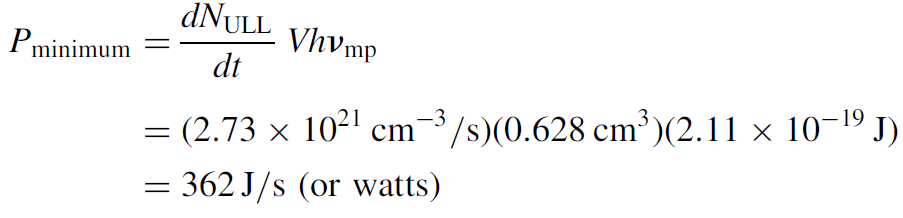
This may seem like a small pump power, especially to anyone who has worked with YAG lasers and has seen the large lamps and power supplies used to drive these systems, but we must now depart from our ideal laser analysis and realize that only a small amount of electrical energy delivered to the lamp is actually converted to pump energy in the YAG system. A typical figure for an optimized optically pumped YAG laser would be around 3%, so the required electrical power supplied to the lamp would be 12.1 kW of power! When pumped by a flash lamp, this represents 12.1 J of energy discharged within 1 ms, obtained easily with a small capacitor and flash lamp. The approximate figure calculated here for the pump power required has been verified in the laboratory to be within 40% of the actual energy required for a flash lamp-pumped YAG laser with these exact parameters.

     In a real laser, 100% of the pump light does not translate into pump energy for the laser (otherwise, the laser described above would indeed operate with 362 W of input). Most gas lasers have overall efficiencies (defined as optical power output divided by electrical power input) of well under 1%. Reasons for low efficiency include the efficiency of the pump source itself at converting electrical energy into optical output, the efficiency with which pump light is coupled into the lasing medium, the absorption efficiency of the lasing material, and the quantum efficiency of the atomic system. The efficiency of conversion of electrical energy into optical output (denoted η_optical) depends on the lamp technology employed (for an optically pumped laser), which can range from a flash lamp to another laser. Use of a laser diode as an optical pump can lead to conversion efficiencies of up to 50%, while the use of halogen lamps (which may be used with YAG) results in poor efficiency since the lamp itself converts at most 10% of the electrical input power to visible light, with the majority of input energy being converted into heat and infrared radiation. Blackbody-type sources have the worst efficiencies at conversion, while gas discharges and laser diodes have progressively higher efficiencies. Coupling of the pump light to the laser medium (denoted η_coupling) is highly dependent on the geometry of the laser medium. Many small solid-state lasers pumped by laser diodes are pumped from one end, where the pump beam passes through the HR itself to enter the crystal as depicted in Figure 1.1. The HR is designed to be transparent at the pump wavelength and fully reflective at the wavelength of the laser rod. If all the pump light is not absorbed in the rod, the OC can also be designed to reflect leftover pump light back into the rod for higher efficiency. Larger crystals, as employed in high-power diode-pumped lasers, are often side pumped with arrays of small laser diodes (mounted on bars of copper for good heat conduction) which surround the rod on all sides. Where lamps (either continuous arc or flash types) are used as a pumping source, reflectors are used to focus as much light as possible from the lamp(s) to the rod. In a single-lamp configuration, the reflector is usually elliptical with both the rod and the lamp at the foci for the ellipse, as shown in Figure 1.2.

Figure 1.1. End on laser diode pumping.

Figure 1.2. Elliptical reflector for lamp pumping.

Absorption efficiency (denoted η_absorption) of the medium varies with the wavelength of the pump source. A laser medium with broad absorption bands is desirable since it can absorb more pump energy from broadband sources such as lamps. Careful choice of wavelength of a laser diode to match an absorption peak in the laser material (e.g., the use of an 808-nm laser diode to pump Nd :YVO₄ , a material called vanadate) can result in absorption efficiencies as high as 80%.

        Finally, the intrinsic quantum efficiency of the atomic system affects the overall efficiency of the laser. In a four-level laser this factor is defined as

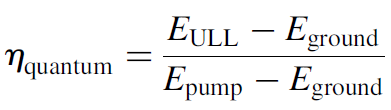 (1.4)

It really represents the energy difference between the pump and ULL and is completely dependent on the particular atomic system. So the overall pump efficiency of the laser (a measure of how well electrical energy is converted to optical output) is a product of all four efficiencies:

   η_pump = η_optical + ‏ η_coupling + ‏ η_absorption + ‏ η_quantum    (1.5)

Example 1.2 Flash lamp-Pumped YAG Laser Consider a flash lamp-pumped YAG laser with the following efficiencies: η_optical = 0.05 (typical for a flash lamps converting to visible and near-IR light), ηcoupling = 0.85 (the elliptical reflector arrangement is quite efficient), η_absorption = 0.3 (poor since the flash lamp is a broadband emission source and the YAG rod absorbs only at a few select bands), η_quantum = 0.68 (an average since the pump energy is spread out across four absorption bands). The overall pump efficiency is just under 1%.

         Now contrast this to a laser diode pumped laser. The quantum efficiency in this case is much more precisely calculated (since it is at a single wavelength) to be

The other efficiencies required are η_optical = 0.33 (typical for a laser diode), η_coupling = 0.95, and η_absorption = 0.8. The overall pump efficiency of this laser is about 22%.

        It is obvious why in recent years the trend in solid-state laser technology has been toward diode-pumped solid-state (DPSS) lasers. Flash lamp pumping is still used, however, where high CW power levels (over 5 or 10 W) or especially high peak powers are required. Diode pumping also lends itself to compact arrangements, while lamp pumping (either continuous arc or flash lamp) invariably involves a large power supply and often requires water cooling.

       Aside from the practical efficiencies already discussed, other factors that affect the efficiency (as well as the minimum pump power required) for real lasers include utilization of the lasing volume by the intracavity laser beam. It is rare that an intracavity laser beam should utilize the entire lasing volume (as we have assumed in our discussion so far), photons inside the cavity usually assume patterns that have a much smaller beam waist in the center of the amplifying medium.