


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات π is the most famous number in mathematics. Forget all the other constants of nature, π will always come at the top of the list. If there were Oscars for numbers, π would get an award every year.
π or pi, is the length of the outside of a circle (the circumference) divided by the length across its centre (the diameter). Its value, the ratio of these two lengths, does not depend on the size of the circle. Whether the circle is big or small, π is indeed a mathematical constant. The circle is the natural habitat for π but it occurs everywhere in mathematics, and in places not remotely connected with the circle.
For a circle of diameter d and radius r :
circumference = πd = 2πr area = πr2
For a sphere of diameter d and radius r :
surface area = πd2 = 4 πr2
volume = 4/3 πr3
Archimedes of Syracuse
The ratio of the circumference to the diameter of a circle was a subject of ancient interest. Around 2000 BC the Babylonians made the observation that the circumference was roughly 3 times as long as its diameter.
It was Archimedes of Syracuse who made a real start on the mathematical theory of π in around 225 BC. Archimedes is right up there with the greats. Mathematicians love to rate their co-workers and they place him on a level with Carl Friedrich Gauss (The ‘Prince of Mathematicians’) and Sir Isaac Newton. Whatever the merits of this judgment it is clear that Archimedes would be in any mathematics Hall of Fame. He was hardly an ivory tower figure though – as well as his contributions to astronomy, mathematics and physics, he also designed weapons of war, such as catapults, levers and ‘burning mirrors’, all used to help keep the Romans at bay. But by all accounts he did have something of the absent-mindedness of the professor, for what else would induce him to leap from his bath and run naked down the street shouting ‘Eureka’ at discovering the law of buoyancy in hydrostatics? How he celebrated his work on π is not recorded.
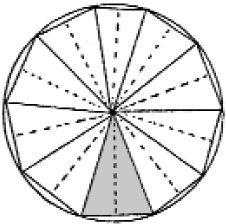
Given that π is defined as the ratio of its circumference to its diameter, what does it have to do with the area of a circle? It is a deduction that the area of a circle of radius r is πr2, though this is probably better known than the circumference/diameter definition of π. The fact that π does double duty for area and circumference is remarkable.

How can this be shown? The circle can be split up into a number of narrow equal triangles with base length b whose height is approximately the radius r. These form a polygon inside the circle which approximates the area of the circle. Let’s take 1000 triangles for a start. The whole process is an exercise in approximations. We can join together each adjacent pair of these triangles to form a rectangle (approximately) with area b × r so that the total area of the polygon will be 500 × b × r. As 500 × b is about half the circumference it has length πr, the area of the polygon is πr × r = πr 2. The more triangles we take the closer will be the approximation and in the limit we conclude the area of the circle is. πr 2.
Archimedes estimated the value of π as bounded between 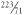 and
and 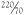 . And so it is to Archimedes that we owe the familiar approximation 22/7 for the value of π. The honour for designating the actual symbol π goes to the little known William Jones, a Welsh mathematician who became Vice President of the Royal Society of London in the 18th century. It was the mathematician and physicist Leonhard Euler who popularized π in the context of the circle ratio.
. And so it is to Archimedes that we owe the familiar approximation 22/7 for the value of π. The honour for designating the actual symbol π goes to the little known William Jones, a Welsh mathematician who became Vice President of the Royal Society of London in the 18th century. It was the mathematician and physicist Leonhard Euler who popularized π in the context of the circle ratio.
The exact value of π
We can never know the exact value of π because it is an irrational number, a fact proved by Johann Lambert in 1768. The decimal expansion is infinite with no predictable pattern. The first 20 decimal places are 3.14159265358979323846…The value of √10 used by the Chinese mathematicians is 3.16227766016837933199 and this was adopted around AD 500 by Brahmagupta. This value is in fact little better than than the crude value of 3 and it differs in the second decimal place from π.
π can be computed from a series of numbers. A well known one is though this is painfully slow in its convergence on π and quite hopeless for calculation. Euler found a remarkable series that converges to π:

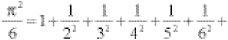
The self-taught genius Srinivasa Ramanujan devised some spectacular approximating formulae for π. One involving only the square root of 2 is:

Mathematicians are fascinated by π. While Lambert had proved it could not be a fraction, in 1882 the German mathematician Ferdinand von Lindemann solved the most outstanding problem associated with π. He showed that π is ‘transcendental’; that is, π cannot be the solution of an algebraic equation (an equation which only involves powers of x). By solving this ‘riddle of the ages’ Lindemann concluded the problem of ‘squaring the circle’. Given a circle the challenge was to construct a square of the same area using only a pair of compasses and a straight edge. Lindemann proved conclusively that it cannot be done. Nowadays the phrase squaring the circle is the equivalent of an impossibility.
The actual calculation of π continued apace. In 1853, William Shanks claimed a value correct to 607 places (actually correct up to only 527). In modern times the quest for calculating π to more and more decimal places gained momentum through the modern computer. In 1949, π was calculated to 2037 decimal places, which took 70 hours to do on an ENIAC computer. By 2002, π had been computed to a staggering 1,241,100,000,000 places, but it is an ever growing tail. If we stood on the equator and started writing down the expansion of π, Shanks’ calculation would take us a full 14 metres, but the length of the 2002 expansion would take us about 62 laps around the world!
Various questions about π have been asked and aswered. Are the digits of π random? Is it possible to find a predetermined sequence in the expansion? For instance, is it possible to find the sequence 0123456789 in the expansion? In the 1950s this seemed unknowable. No one had found such a sequence in the 2000 known digits of π. L.E.J. Brouwer, a leading Dutch mathematician, said the question was devoid of meaning since he believed it could not be experienced. In fact these digits were found in 1997 beginning at the position 17,387,594,880, or, using the equator metaphor, about 3000 miles before one lap is completed. You will find ten sixes in a row before you have completed 600 miles but will have to wait until one lap has been completed and gone a further 3600 miles to find ten sevens in a row.
π in poetry
If you really want to remember the first values in the expansion of π perhaps a little poetry will help. Following the tradition of teaching mathematics in the ‘mnemonic way’ there is a brilliant variation of Edgar Allen Poe’s poem ‘The Raven’ by Michael Keith.

The letter count of each successive word in Keith’s version provides the first 740 digits of π.
The importance of π
What is the use of knowing π to so many places? After all, most calculations only require a few decimal places; probably no more than ten places are needed for any practical application, and Archimedes’ approximation of 22/7 is good enough for most. But the extensive calculations are not just for fun. They are used to test the limits of computers, besides exerting a fascination on the group of mathematicians who have called themselves the ‘friends of pi’.
Perhaps the strangest episode in the story of π was the attempt in the Indiana State Legislature to pass a bill that would fix its value. This occurred at the end of the 19th century when a medical doctor Dr E.J. Goodwin introduced the bill to make π ‘digestible’. A practical problem encountered in this piece of legislation was the proposer’s inability to fix the value he wanted. Happily for Indiana, the folly of legislating on π was realized before the bill was fully
the condensed idea
When the π was opened




|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|