Sudoku unlocked

In Sudoku we are given a 9×9 grid with some numbers filled in. The object is to fill in the rest using the given numbers as clues. Each row and each column should contain exactly one of the digits 1, 2, 3, …, 9, as do the small constituent 3×3 squares.

It is believed that Sudoku (meaning ‘single digits’) was invented in the late 1970s. It gained popularity in Japan in the 1980s before sweeping to mass popularity by 2005. The appeal of the puzzle is that, unlike crosswords, you don’t have to be widely read to attempt them but, like crosswords, they can be compelling. Addicts of both forms of self-torture have much in common.

3×3 Latin squares

A square array containing exactly one symbol in each row and each column is called a Latin square. The number of symbols equals the size of the square and is called its ‘order’. Can we fill out a blank 3×3 grid so that each row and column contains exactly one of the symbols a, b and c? If we can, this would be a Latin square of order 3.

In introducing the concept of a Latin square, Leonhard Euler called it a ‘new kind of magic square’. Unlike magic squares, however, Latin squares are not concerned with arithmetic and the symbols do not have to be numbers. The reason for the name is simply that the symbols used to form them are taken from the Latin alphabet, while Euler used Greek with other squares.

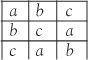
A 3×3 Latin square can be easily written down.

If we think of a, b and c as the days of the week Monday, Wednesday and Friday, the square could be used to schedule meetings between two teams of people. Team One is made up of Larry, Mary and Nancy and Team Two of Ross, Sophie and Tom.

For example, Mary from Team One, has a meeting with Tom from Team Two on Monday (the intersection of the M row with the T column is a = Monday). The Latin square arrangement ensures a meeting takes place between each pair of team members and there is no clash of dates.

This is not the only possible 3×3 Latin square. If we interpret A, B and C as topics discussed at the meetings between Team One and Team Two, we can produce a Latin square which ensures each person discusses a different topic with a member of the other team.

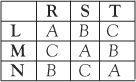
So Mary from Team One discusses topic C with Ross, topic A with Sophie and topic B with Tom.

But when should the discussions take place, between who, and on what topic? What would be the schedule for this complex organization? Fortunately the two Latin squares can be combined symbol by symbol to produce a composite Latin Square in which each of the possible nine pairs of days and topics occurs in exactly one position.

Another interpretation for the square is the historical ‘nine officers problem’ in which nine officers belonging to three regiments a, b and c and of three ranks A, B and C are placed on the parade ground so that each row and column contains an officer of each regiment and rank. Latin squares which combine in this way are called ‘orthogonal’. The 3×3 case is straightforward but finding pairs of orthogonal Latin squares for some larger ones is far from easy. This is something Euler discovered.

In the case of a 4×4 Latin Square, a ‘16 officers problem’ would be to arrange the 16 court cards in a pack of cards in a square in such a way that there is one rank (Ace, King, Queen or Jack) and one suit (spades, clubs, hearts or diamonds) in each row and column. In 1782 Euler posed the same problem for ‘36 officers’. In essence he was looking for two orthogonal squares of order 6. He couldn’t find them and conjectured there were no pairs of orthogonal Latin squares of orders 6, 10, 14, 18, 22 … Could this be proved?

Along came Gaston Tarry, an amateur mathematician who worked as a civil servant in Algeria. He scrutinized examples and by 1900 had verified Euler’s conjecture in one case: there is no pair of orthogonal Latin squares of order 6. Mathematicians naturally assumed Euler was correct in the other cases 10, 14, 18, 22 …

In 1960, the combined efforts of three mathematicians stunned the mathematical world by proving Euler wrong in all the other cases. Raj Bose, Ernest Parker and Sharadchandra Shrikhande proved there were indeed pairs of orthogonal Latin squares of orders 10, 14, 18, 22, … The only case where Latin squares do not exist (apart from trivial ones of orders 1 and 2) is order 6.

We’ve seen that there are two mutually orthogonal order 3 Latin squares. For order 4 we can produce three squares which are mutually orthogonal to each other. It can be shown that there are never more than n − 1 mutually orthogonal Latin squares of order n, so for n = 10, for example, there cannot be more than nine mutually orthogonal squares. But finding them is a different story. To date, no one has been able to even produce three Latin squares of order 10 that are mutually orthogonal to each other.

Are Latin squares useful?

R.A. Fisher, an eminent statistician, saw the practical use of Latin squares. He used them to revolutionize agricultural methods during his time at Rothamsted Research Station in Hertfordshire, UK.

Fisher’s objective was to investigate the effectiveness of fertilizers on crop yield. Ideally we would want to plant crops in identical soil conditions so that soil quality wasn’t an unwanted factor influencing crop yield. We could then apply the different fertilizers safe in the knowledge that the ‘nuisance’ of soil quality was eliminated. The only way of ensuring identical soil conditions would be to use the same soil – but it is impractical to keep digging up and replanting crops. Even if this were possible different weather conditions could become a new nuisance.

A way round this is to use Latin squares. Let’s look at testing four treatments. If we mark out a square field into 16 plots we can envisage the Latin square as a description of the field where the soil quality varies ‘vertically’ and ‘horizontally’.

The four fertilizers are then applied at random in the scheme labelled a, b, c and d, so exactly one is applied in each row and column in an attempt to remove the variation of soil quality. If we suspect another factor might influence crop yield, we could deal with this too. Suppose we think that the time of day of apllying treatment is a factor. Label four time zones during the day as A, B, C and D and use orthogonal Latin squares as the design for a scheme to gather data. This ensures each treatment and time zone is applied in one of the plots. The design for the experiment would be:

Other factors can be screened out by going on to create even more elaborate Latin square designs. Euler could not have dreamt of the solution to his officers’ problem being applied to agricultural experiments.

the condensed idea

Sudoku revealed