Fermat’s last theorem is about a Diophantine equation, the kind of equation which poses the stiffest of all challenges. These equations demand that their solutions be whole numbers. They are named after Diophantus of Alexandria whose Arithmetica became a milestone in the theory of numbers. Pierre de Fermat was a 17th-century lawyer and government official in Toulouse in France. A versatile mathematician, he enjoyed a high reputation in the theory of numbers, and is most notably remembered for the statement of the last theorem, his final contribution to mathematics. Fermat proved it, or thought he had, and he wrote in his copy of Diophantus’s Arithmetica ‘I have discovered a truly wonderful proof, but the margin is too small to contain it.’

Fermat solved many outstanding problems, but it seems that Fermat’s last theorem was not one of them. The theorem has occupied legions of mathematicians for three hundred years, and has only recently been proved. This proof could not be written in any margin and the modern techniques required to generate it throw extreme doubt on Fermat’s claim.

The equation x + y = z

How can we solve this equation in three variables x, y and z? In an equation we usually have one unknown x but here we have three. Actually this makes the equation x + y = z quite easy to solve. We can choose the values of x and y any way we wish, add them to get z and these three values will give a solution. It is as simple as that.

For example if we choose x = 3 and y = 7, the values x = 3, y = 7 and z = 10 make a solution of the equation. We can also see that some values of x, y and z are not solutions of the equation. For example x = 3, y = 7 and z = 9 is not a solution because these values do not make the left-hand side x + y equal the right hand side z.

The equation x² + y² = z²

We’ll now think about squares. The square of a number is that number multiplied by itself, the number which we write as x². If x = 3 then x² = 3 × 3 = 9. The equation we are thinking of now is not x + y = z, but

x² + y² = z²

Can we solve this as before, by choosing values for x and y and computing z? With the values x = 3 and y = 7, for example, the left-hand side of the equation is 3² + 7² which is 9 + 49 = 58. For this z would have to be the square root of 58 (z = √58) which is approximately 7.6158. We are certainly entitled to claim that x = 3, y = 7 and z = √58 is a solution of x² + y² = z² but unfortunately Diophantine equations are primarily concerned with whole number solutions. As √58 is not a whole number, the solution x = 3, y = 7 and z = √58 will not do.

The equation x² + y² = z² is connected with triangles. If x, y and z represent the lengths of the three sides of a right-angled triangle they satisfy this equation. Conversely, if x, y and z satisfy the equation then the angle between x and y is a right angle. Because of the connections with Pythagoras’s theorem solutions for x, y and z are called Pythagorean triples.

How can we find Pythagorean triples? This is where the local builder comes to the rescue. Part of the builder’s equipment is the ubiquitous 3–4–5 triangle. The values x = 3, y = 4 and z = 5 turn out to be a solution of the kind we are looking for because 3² + 4² = 9 + 16 = 5². From the converse, a triangle with dimensions 3, 4 and 5, must include a right angle. This is the mathematical fact that the builder uses to build his walls at right angles.

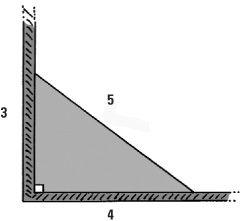
In this case we can break up a 3 × 3 square, and wrap it around a 4 × 4 square to make a 5 × 5 square.

There are other whole number solutions x² + y² = z². For example x = 5, y = 12 and z = 13 is another solution because 5² +12² = 13² and in fact there are an infinite number of solutions to the equation. The builder’s solution x = 3, y = 4 and z = 5 holds pride of place since it is the smallest solution, and is the only solution composed of consecutive whole numbers. There are many solutions where two numbers are consecutive, such as x = 20, y = 21 and z = 29 as well as x = 9, y = 40 and z = 41, but no others with all three.

From feast to famine

It looks like a small step to go from x² + y² = z² to x3 + y³ = z³. So, following the idea of reassembling one square around another to form a third square, can we pull off the same trick with a cube? Can we reassemble one cube around another to make a third? It turns out this can’t be done. The equation x² + y² = z² has an infinite number of different solutions but Fermat was unable to find even one whole number example of x³ + y³ = z³. Worse was to follow, and Leonhard Euler’s lack of findings led him to phrase the last theorem:

There is no solution in whole numbers to the equation xⁿ + yⁿ = zⁿ for all values of n higher than 2.

One way to approach the problem of proving this is to start on the low values of n and move forward. This was the way Fermat went to work. The case n = 4 is actually simpler than n = 3 and it is likely Fermat had a proof in this case. In the 18th and 19th centuries, Euler filled in the case n = 3, Adrien-Marie Legendre completed the case n = 5 and Gabriel Lamé proved the case n = 7. Lamé initially thought he had a proof of the general theorem but was unfortunately mistaken.

Ernst Kummer was a major contributor and in 1843 submitted a manuscript claiming he had proved the theorem in general, but Dirichlet pointed out a gap in the argument. The French Academy of Sciences offered a prize of 3000 francs for a valid proof, eventually awarding it to Kummer for his worthy attempt. Kummer proved the theorem for all primes less than 100 (and other values) but excluding the irregular primes 37, 59 and 67. For example, he could not prove there were no whole numbers which satisfied x⁶⁷ + y⁶⁷ = z⁶⁷. His failure to prove the theorem generally opened up valuable techniques in abstract algebra. This was perhaps a greater contribution to mathematics than settling the question itself.

Ferdinand von Lindemann, who did prove that the circle could not be squared claimed to have proved the theorem in 1907 but was found to be in error. In 1908 Paul Wolfskehl bequeathed a 100,000 marks prize to be awarded to the first provider of a proof, a prize made available for 100 years. Over the years, something like 5000 proofs have been submitted, checked, and all returned to the hopefuls as being false.

The proof

While the link with Pythagoras’s theorem only applies for n = 2, the link with geometry proved the key to its eventual proof. The connection was made with the theory of curves and a conjecture put forward by two Japanese mathematicians Yutaka Taniyama and Goro Shimura. In 1993 Andrew Wiles gave a lecture on this theory at Cambridge and included his proof of Fermat’s theorem. Unhappily this proof was wrong.

The similarly named French mathematician André Weil dismissed such attempts. He likened proving the theorem with climbing Everest and added that if a man falls short by 100 yards he has not climbed Everest. The pressure was on. Wiles cut himself off and worked on the problem incessantly. Many thought Wiles would join that throng of the nearly people.

With the help of colleagues, however, Wiles was able to excise the error and substitute a correct argument. This time he convinced the experts and proved the theorem. His proof was published in 1995 and he claimed the Wolfskehl prize just inside the qualifying period to become a mathematical celebrity. The ten-year-old boy sitting in a Cambridge public library reading about the problem years before had come a long way.

the condensed idea

Proving a marginal point