


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-11-2021
Date: 15-10-2021
Date: 16-9-2021
|
Another technique used to avoid the problems of the plurality method is sequential voting. In this scheme a vote is taken, as a consequence a new set of candidates is selected; then a new vote is taken. The aim is to reduce the set of candidates to a manageable size—often to size two. The original election is again called a primary, but in this case all the candidates run in the primary election, not just those in one party.
For example, when the President of France is to be elected, there is a primary election for all the candidates. Each voter can select one candidate, and the numbers of votes for each candidate are counted. Later there is another election; there are two candidates, the two candidates who received the most votes in the primary. This second (runoff) election is decided by the majority method. A similar method is used in electing the President of the Ukraine, and in a number of other situations.
We shall refer to this as the runoff method or plurality runoff method. The two top candidates are decided by plurality vote; all other candidates are eliminated; then a majority vote is taken.
In the real world, the preference list is not fixed. There is usually a delay after the primary, and more campaigning takes place. As a result of this the preference lists may change. But for simplicity’s sake we shall ignore this for the moment, and assume that every voter has an order of preference between the candidates that remains fixed throughout the voting process. We define the preference profile of an election to be the set of all the voters’ preference lists. This can conveniently be written in a table. For example, say there are three candidates, A, B, C, and suppose:
5 voters like A best, then B, then C;
7 voters like B best, then A, then C;
4 voters like A best, then C, then B;
3 voters like C best, then B, then A;
no voters like B, then C, then A;
no voters like C, then B, then A.
We can represent this as

but we shall usually omit zero columns.)
In the primary election, each elector votes for the candidate he or she likes best.
In the example, A would receive nine votes—five from those with preference list ABC, and four from those with list ACB. In general, a candidate receives the votes of those who put that candidate first in the preference list. Then the two candidates with the most votes go on to the main election. To work out the votes, you could delete all the other candidates from the electors’ lists, so that everybody has a list with just two members. And remember, in the real world, some electors will change their preferences before the runoff election.
Sample Problem 1.1 Suppose the preference profile of an election is
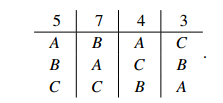
What is the result of the election in the following cases?
(i) The majority method is used.
(ii) The plurality method is used.
(iii) The runoff method is used.
Solution. A receives nine votes, B receives seven, C receives three. So (i) there is no majority winner (as there are 19 voters, 10 votes would be needed), and (ii) A is the plurality winner. In a primary election, A and B are selected to contest the runoff. For the runoff, C is deleted, and the preference profile becomes

So B wins the runoff.
Modifications of this method are also used. When the city of Carbondale, Illinois, elects its Mayor, there is a primary election when there are more than four Mayoral candidates. In the final election, the candidates are the four original candidates who received the most primary votes, and the plurality method is used.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|