المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | منحني تكراري ذو قمتين Binomial Curve |
 2379
 02:25 صباحاً
التاريخ: 20-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 338|
أقرأ أيضاً
التاريخ: 20-2-2021
1442
التاريخ: 17-11-2015
1796
التاريخ: 1-4-2021
3322
التاريخ: 14-2-2016
2173
|
نبدأ بتمثيله البياني كما في الشكل .
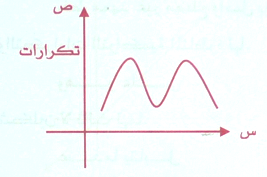
انه كالجمل ذي السنامين والتفسير كما يلي : السبب الوحيد لوجود قمتين هو عدد تجانس المجتمع الإحصائي أو العينة التي يقوم الباحث بدراستها والتي تحتوي مجموعتين مختلفتين متداخلتين كدراسة مجتمع طلبة إحدى الكليات المكون من طلاب وطالبات وبعد فصلهما تحصل على توزيعين مختلفين تماماً تمثل كل منها قمة من القمتين .
واحياناً تتعدد القيم لتباين المجموعات المكونة للمجتمع الإحصائي .
|
|
|
|
الصين.. طريقة لمنع تطور قصر النظر لدى تلاميذ المدارس
|
|
|
|
|
|
|
ماذا سيحدث خلال كسوف الشمس يوم السبت؟
|
|
|
|
|
|
|
بمشاركة مجتمعيّة واسعة .. اختتام فعاليات المجلس العلوي الثقافي السنوي الثاني
|
|
|
