


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 26-1-2017
Date: 23-12-2015
Date: 22-12-2015
|
Entropy on Light-like Surfaces
So far we have considered the entropy that passes through space-like surfaces. We will see that it is most natural to define holographic entropy bounds on light-like surfaces[3] as opposed to space-like surfaces. Under certain circumstances the entropy bounds of light-like surfaces can be translated to space-like surfaces, but not always. The case described above is one of those cases where a space-like bound is derivable.
Let us start with an example in asymptotically flat space-time. We assume that flat Minkowski coordinates X+,X−, xi can be defined at asymptotic distances. In this chapter we will revert to the usual convention in which X+ is used as a light cone time variable. We will now define a “lightsheet”. Consider the set of all light rays which lie in the surface X+ = X+0 in the limit X− → +∞. In ordinary flat space this congruence of rays defines a flat three-dimensional light-like surface. In general, they define a light-like surface called a light sheet. The light sheet will typically have singular caustic lines, but can be defined in a unique way[4]. When we vary X+0 the light sheets fill all space-time except for those points that lie behind black hole horizons.
Now consider a space-time point p. We will assign it light cone coordinates as follows. If it lies on the light sheet X+0 we assign it the value X+ = X+0 .Also if it lies on the light ray which asymptotically has transverse coordinate xi0 we assign it xi = xi0. The value of X that we assign will not matter. The two-dimensional xi plane is called the Screen. Next assume a black hole passes through the light sheet X+0 .The stretched

Fig. 1.1. Light propagating on light-like surface X+ = constant.

Fig. 1.2. Family of light rays on fixed X+ surface in presence of black hole.
horizon of the black hole describes a two-dimensional surface in the three dimensional light sheet as shown in Figure 1.2. Each point on the stretched horizon has unique coordinates X+, xi, as seen in Figure 1.3. More generally if there are several black holes passing through the light sheet we can map each of their stretched horizons to the screen in a single valued manner.
Since the entropy of the black hole is equal to 1/4G times the area of the horizon we can define an entropy density of 1/4G on the stretched horizon. The mapping to the screen then defines an entropy density in the xi plane, σ(x).I t is a remarkable fact that σ(x) is always less than or equal to 1/4G.
To prove that σ(x) ≤ 1/4G we make use of the focusing theorem of general relativity. The focusing theorem depends on the positivity of energy and is based on the tendency for light to bend around regions of nonzero energy. Consider a bundle of light rays with cross sectional area α.The light rays
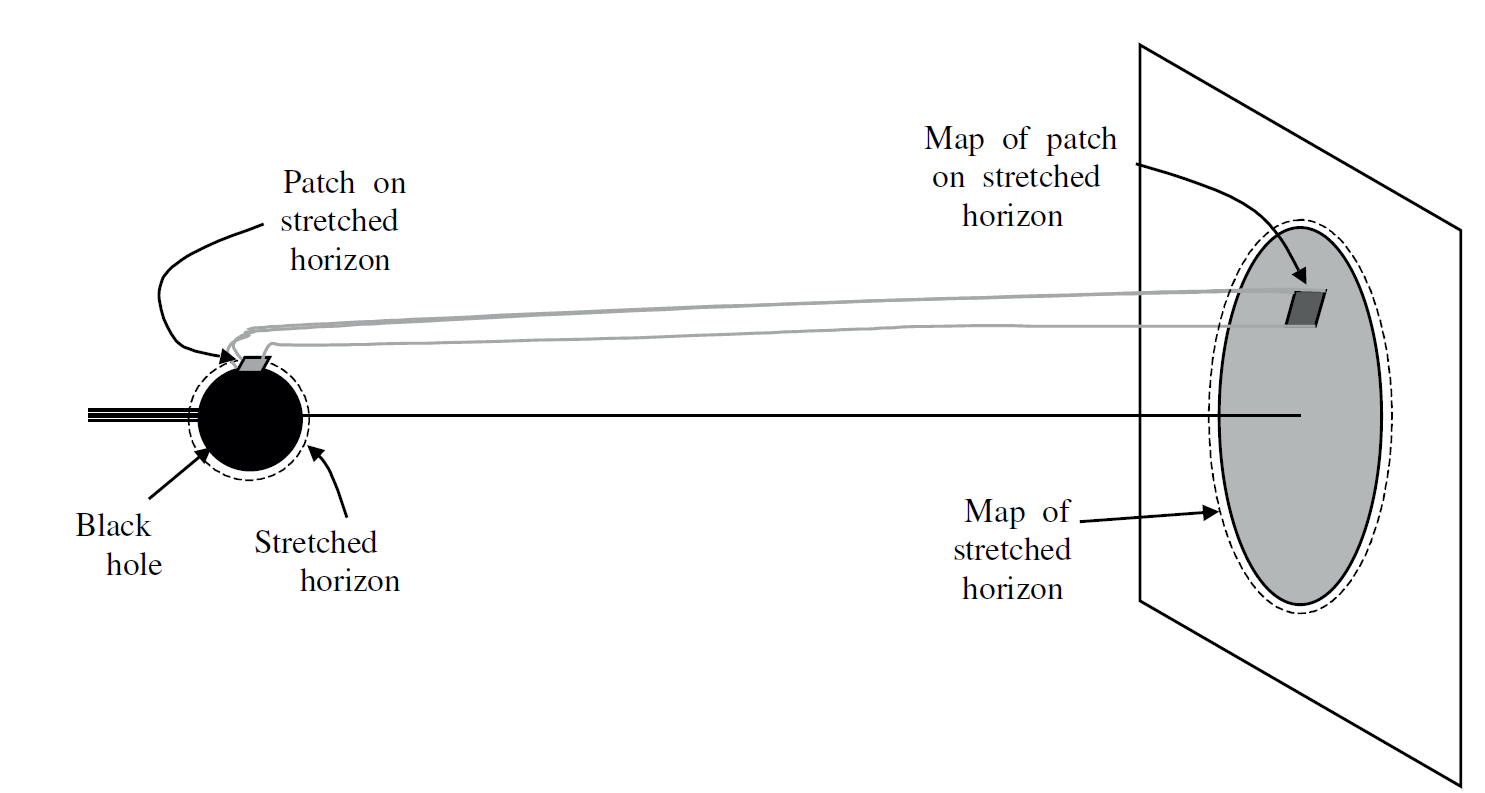
Fig. 1.3. Image of “stretched horizon” on asymptotic screen.
are parameterized by an affine parameter λ. The focusing theorem says that
 (1.1)
(1.1)
Consider a bundle of light rays in the light sheet which begin on the stretched horizon and go off to X− = ∞. Since the light rays defining the light sheet are parallel in the asymptotic region dα/dλ → 0. The focusing theorem tells us that as we work back toward the horizon, the area of the bundle decreases. It follows that the image of a patch of horizon on the screen is larger than the patch itself. The holographic bound immediately follows.
 (1.2)
(1.2)
This is a surprising conclusion. No matter how we distribute the black holes in three-dimensional space, the image of the entropy on the screen always satisfies the entropy bound equation 1.2. An example which helps clarify how this happens involves two black holes. Suppose we try to hide one of them behind the other along the X− axis, thus doubling the entropy density in the x plane. The bending and focusing of light always acts as in Figures 1.4 to prevent σ(x) from exceeding the bound. These considerations lead us to the more general conjecture that for any system,
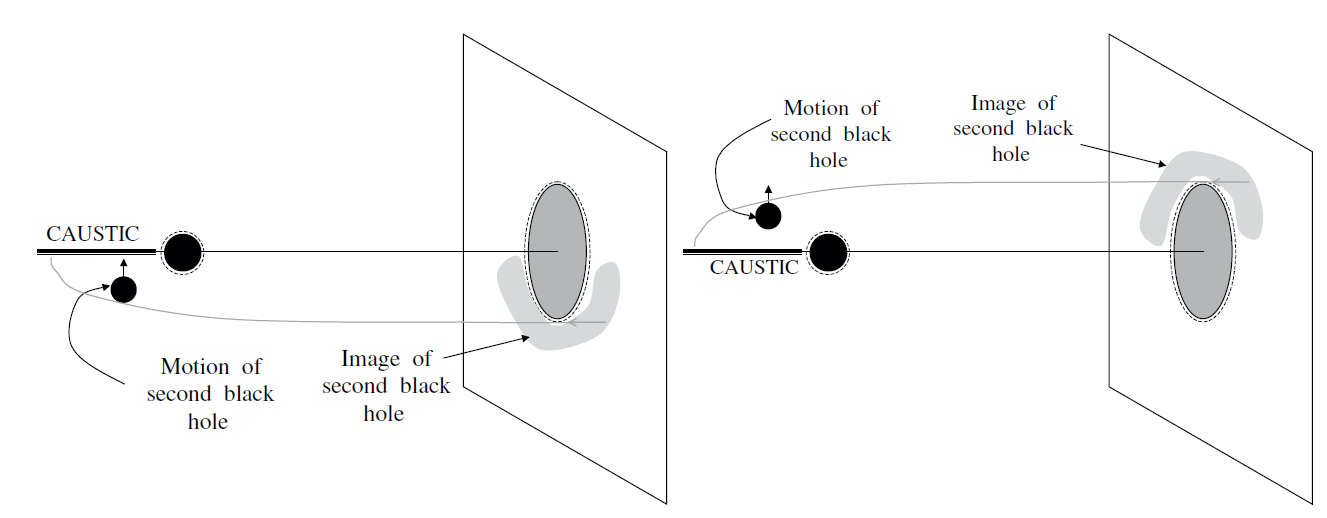
Fig. 1.4. Initial and later motions and images of second black hole.
when it is mapped to the screen the entropy density obeys the bound in equation 1.2. Thus far we have assumed asymptotically flat boundary conditions. This allowed us to choose the screen so that the light rays forming the light sheet intersect the screen at right angles. Equivalently da/dλ equals zero at the screen. We note for future use that the conclusions concerning the entropy bound would be unchanged if we allowed screens for which the light rays were diverging as we move outward, i.e. da/dλ > 0. However, if we attempt to use screens for which the light rays are converging then the argument fails. This will play an important role in generalizing the holographic bound to more general geometries.
_______________________________________________________
Aside: Apparent motions
Consider a single point particle external to the black hole undergoing motions near a caustic. Examine the projection of those motion upon the screen, demonstrated in Figures 1.7. One sees that due to gravitational lensing, the image of the particle can move at arbitrarily large speeds!

Fig. 1.7. Initial and later path and image during “slow” motion near caustic.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|