


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-02-04
التاريخ: 2024-01-27
التاريخ: 5-10-2020
التاريخ: 2023-02-05
|
سبق أن ناقشنا التصادم الذي يلتصق فيه جسمان متصادمان معا. في هذه الحالة تعين السرعة النهائية باستخدام مبدأ حفظ كمية التحرك. وبصورة خاصة، دعنا نعتبر جسيمًا كتلته m1 وسرعته 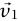 ان يتصادم مع جسيم كتلته m2 كان ساكنا في البداية. إذا التصق الجسمان معًا، فإن السرعة النهائية تكون
ان يتصادم مع جسيم كتلته m2 كان ساكنا في البداية. إذا التصق الجسمان معًا، فإن السرعة النهائية تكون 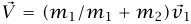 وتكون طاقة الحركة النهائية هي:
وتكون طاقة الحركة النهائية هي:
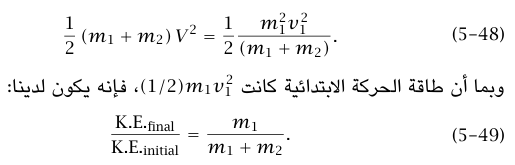
وبناءً على ذلك، إذا كان m1 = m2 فإننا نجد أن نصف طاقة الحركة الأصلية قد فقد في التصادم. تكون الطاقة المفقودة قد تحولت إلى طاقة حركة جزيئية وطاقة جهد داخلية للجسمين المتصادمين. وحقيقة أن هذين الجسمين يلتصقان معًا تضمن وجود آلية ما لتحويل طاقة حركة عيانية (ماكروسكوبية) إلى طاقة حركة وجهد مجهرية (ميكروسكوبية) «غير مرئية». إذا لم توجد مثل هذه الآلية، فإن الجسمين المتصادمين لا يمكن أن يلتصقا معًا.
التصادم الذي تكون فيه طاقة الحركة الماكروسكوبية النهائية أصغر من طاقة الحركة الماكروسكوبية الابتدائية يسمى تصادمًا غير مرن. إذا كانت طاقة الحركة النهائية مساوية لطاقة الحركة الابتدائية، فإن التصادم يسمى تصادما مرنا. التصادم بين كرتين ملساوين من الصلب غالبًا ما يكون مرنا تمامًا (تام المرونة). هناك، طبعًا، درجات متغيرة لعدم المرونة؛ على سبيل المثال، يمكن أن تكون طاقة الحركة النهائية أقل قليلًا من طاقة الحركة الابتدائية، حتى لو كان الجسمان المتصادمان لا يلتصقان معًا.
وعندما يتصادم جسيمان، فإنه يوجد كما سبق أن (ناقشنا) حالات نهائية عديدة ممكنة ومتسقة مع مبدأ حفظ كمية الحركة. ومن السهل توضيح أنه من بين جميع هذه الحالات تكون الحالة الأقل طاقة حركة هي الحالة التي يكون فيها للجسيمين نفس السرعة النهائية؛ أي إنهما يلتصقان معًا. التصادم الذي يلتصق فيه الجسيمان معا يسمى التصادم غير المرن تمامًا (أو غير تام المرونة). بدقة أكثر، لا بد أن نسمي مثل هذا التصادم أكثر تصادم غير مرن؛ لأنه بصورة عامة لا يزال هناك بعض الطاقة الحركية الماكروسكوبية في الحالة النهائية. حفظ كمية التحرك يضع حدا لكمية طاقة الحركة التي يمكن تحولها إلى الشكل المجهري. وعندما يلتصق معًا جُسيمان متصادمان فإن طاقة الحركة النهائية تكون P2/2M؛ حيث P كمية التحرك الكلية هي وM الكتلة الكلية.
إذا كان النظام خاليًا من أي قوى خارجية، فإن كمية التحرك الكلية تكون محافظة. وبخلاف الطاقة، لا يمكن تحويل كمية التحرك إلى صورة «غير مرئية»، ولن يحمل الاهتزاز الجزيئي العشوائي أي كمية تحرك صافية لأن جزيئات عديدة تتحرك في اتجاه ما، وأخرى مثلها تتحرك في اتجاه آخر. إذا كانت هناك سرعة غير عشوائية «سرعة انسياق» متراكبة على الاهتزاز، فإن الجسم بأكمله سوف يتحرك بسرعة الانسياق هذه؛ وبذلك تكون كمية التحرك كلها مرئية، ويمكننا توقع أن تكون كمية التحرك محافظة حتى عندما لا تكون الطاقة (ظاهريًّا) كذلك ، بشرط ألا تؤثر أي قوة خارجية على النظام.

شكل 5–12: قبل وبعد تصادم مرن في بعد واحد.
رأينا أن حفظ كمية التحرك يحدد تمامًا الحالة النهائية في تصادم غير مرن تماما. ثَمَّة موقف آخر مهم تكون فيه الحالة النهائية محددة تمامًا؛ وهو التصادم المرن في بعد واحد. ونقصد «بالبعد الواحد» أن توجد جميع الجسيمات على خط، مثل المحور x. توجد سرعتان مجهولتان في الحالة النهائية (نسميهما f1v وv2f). ويفرض حفظ كمية التحرك شرطًا واحدًا على المجهولين، إذا كنا نطلب أيضًا حفظًا للطاقة، يكون لدينا معادلة أخرى؛ ومن ثم تحدد الحالة النهائية.
للتبسيط، نفترض أن m2 ساكن في البداية، وأن m1 في البداية كانت سرعته v1i. حفظ كمية التحرك يتطلب:

لإيجاد المجهول v2f. بقليل من الجبر يمكن إعادة كتابة هذه المعادلة على الصورة:
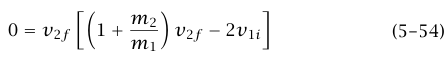
وجذراها هما 0 = v2f و v2f = 2v1i / (1 + m1/m2)ما المغزى الفيزيائي لهذين الجذرين؟ إذا كان 0 = v2f فإن المعادلة (52–5) تعني ضمنا أن v2f = v1f. هذا الحل، الذي فيه تكون السرعتان النهائيتان لكلا الجسيمين متماثلتين مع سرعتيهما الابتدائيتين، يفي بوضوح حفظ الطاقة وكمية التحرك، لكنه فيزيائيا يكون ذا معنى فقط إذا لم يكن هناك تآثر بين الجسيمين (بحيث يمكن للكتلة m1 أن تعبر خلال m2 دون أن تبذل قوة عليها).
الحل الآخر هو:

هي المهمة فيزيائيا.
من المفيد تعليميًّا فحص المعادلتين (55–5) و(56–5) في حالات حدية متنوعة، لكي نرى ما إذا كانت الصياغتان متَّسقتين مع توقعاتنا. هناك ثلاث حالات حدية يمكن فهمها ببساطة:
(1) افترض أن 1 ≫ 1m/2m (كرة تنس الطاولة تصطدم مباشرةً بكرة بولينج ثابتة). نتوقع أن تظل كرة البولينج ساكنة أساسًا وترتد كرة الطاولة (مثلما ترتد من حائط صلد) بسرعة تساوي سرعتها الابتدائية في المقدار وتُضادُّها في الاتجاه؛ بهذا نتوقع أن يكون v2f = 0 وv1f = – v1i وهو ما يتفق مع المعادلتين (55–5) و(56–5) عندما يكون 1 ≫ 1m/2m.
(2) افترض أن m1 = m2؛ عندئذ تؤدي المعادلتان (55–5) و(56–5) إلى أن يكون v1f = 0 وv2f = – v1i؛ أي إن الجسيمين يتبادلان السرعتين هذا الحل مألوف لدى لاعبي البلياردو ودفع الأقراص، ويمكن فهمه بسهولة بالنظر إلى التصادم من منظور إطار قصوري آخر، نظام مركز الكتلة. سرعة مركز الكتلة هي v1i(1/2)، وفي هذا الإطار يكون التصادم متماثلاً؛ أي إن سرعة الجسيم رقم 1 في البداية هي v1i(1/2) وسرعة الجسيم رقم 2 في البداية هي v1i(1/2)–. وفي التصادم المرن المتماثل تكون السرعة النهائية لكل جسيم مجرد سالب سرعته الابتدائية؛ ولهذا فإنه في نظام مركز الكتلة تكون السرعة النهائية للجسيم رقم 1 هي v1i(1/2)– والسرعة النهائية للجسيم رقم 2 هي v1i (1/2). لترجمة هذا بلغة الراصد الثابت نضيف v1i(1/2) (سرعة مركز الكتلة) إلى كلٌّ من هاتين السرعتين؛ فينتج أن v1f = 0 وv2f = v1i
(3) افترض أن 1 ≪ 1m/2m (كرة بولينج تصطدم مباشرةً بكرة طاولة ساكنة). هذا التصادم يسبب تغيرًا مهملًا في سرعة الجسم الثقيل؛ ولهذا فإن v1f = v1i، وذلك في اتفاق مع المعادلة (56–5). في هذه الحالة يكون لمركز الكتلة بصورة أساسية نفس سرعة الجسم الثقيل؛ أي إن 011 = Vcm. في نظام مركز الكتلة، يقترب الجسم الخفيف من الجسم الثقيل بسرعة v1i –، ثم يرتد (مثلما يرتد من جدار صلد) بسرعة v1f؛ وبناءً على ذلك، من وجهة نظر الراصد الثابت، تتفق v2f = 2v1i مع المعادلة (55–5).
توضح المناقشة السابقة جانبًا مهما من طريقة جيدة لحل المسائل. إذا كان هناك بارامتر ما متغير (مثل m2/m1) في المسألة، فإنه كثيرًا ما يكفي التعليل المنطقي البسيط لتوقع الإجابة بالنسبة إلى قيم خاصة معينة لذلك البارامتر. إذا كان حلّك لا يوافق توقعاتك في هذه الحالات الخاصة، فإنه إما أن يكون حلك خطاً (خطأً جبريًا أو أمرًا ما أكثر جدية؟) أو تكون توقعاتك غير سليمة.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|