
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
تعريف الشغل
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 145 – ص 148
2024-09-18
1646
افترض قوة  مؤثرة على جسيم يتعرّض لإزاحة صغيرة جدًّا
مؤثرة على جسيم يتعرّض لإزاحة صغيرة جدًّا 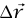 . يعرف الشغل الذي تؤثر به القوة بأنه:
. يعرف الشغل الذي تؤثر به القوة بأنه:
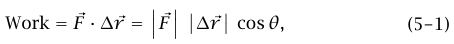
حيث θ هي الزاوية بين  و
و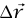 . لاحظ أنه لا يوجد فرق فيما إذا أخذنا θ زاوية داخلية أو خارجية لأن cos θ = cos (360o – θ) الشغل يمكن أن يكون موجبا أو سالبا، اعتمادًا على ما إذا كانت θ بين 0o و90o أو بين °90 و°180؛ وبناءً عليه، إذا كنتَ تدفع صندوقًا إلى أعلى مستوى مائل، فإنك تبذل شغلا موجبًا على الصندوق، والجاذبية تبذل شغلًا سالبًا؛ أما إذا كنت تشد الصندوق كي تمنعه من الانزلاق إلى أسفل السطح المائل، فهنا أنت تبذل شغلًا سالبًا على الصندوق، والجاذبية تبذل شغلًا موجبا. لاحظ أنه إذا كانت °90 = θ (القوة عمودية على الإزاحة)، فإن القوة لا تبذل شغلًا؛ لهذا فإنه إذا تحرك جسيم على سطح أملس، فإن القوة العمودية التي يبذلها السطح لا تبذل شغلًا على الجسيم.
. لاحظ أنه لا يوجد فرق فيما إذا أخذنا θ زاوية داخلية أو خارجية لأن cos θ = cos (360o – θ) الشغل يمكن أن يكون موجبا أو سالبا، اعتمادًا على ما إذا كانت θ بين 0o و90o أو بين °90 و°180؛ وبناءً عليه، إذا كنتَ تدفع صندوقًا إلى أعلى مستوى مائل، فإنك تبذل شغلا موجبًا على الصندوق، والجاذبية تبذل شغلًا سالبًا؛ أما إذا كنت تشد الصندوق كي تمنعه من الانزلاق إلى أسفل السطح المائل، فهنا أنت تبذل شغلًا سالبًا على الصندوق، والجاذبية تبذل شغلًا موجبا. لاحظ أنه إذا كانت °90 = θ (القوة عمودية على الإزاحة)، فإن القوة لا تبذل شغلًا؛ لهذا فإنه إذا تحرك جسيم على سطح أملس، فإن القوة العمودية التي يبذلها السطح لا تبذل شغلًا على الجسيم.

شكل 5–1: حساب الشغل.
تعريف الشغل (المعادلة (1–5)) يمكن استخدامه حتى لو لم تكن الإزاحة صغيرة جدًّا، بشرط ألا تتغيّر القوة  أثناء الإزاحة. إذا تغيَّرت
أثناء الإزاحة. إذا تغيَّرت  فإن التعريف (معادلة (1–5)) يكون ملتبسًا. (ما قيمة
فإن التعريف (معادلة (1–5)) يكون ملتبسًا. (ما قيمة  التي نستخدمها؟) والتعريف «الطبيعي» المفيد والوحيد هو ما يلي:
التي نستخدمها؟) والتعريف «الطبيعي» المفيد والوحيد هو ما يلي:
افترض أن جسيمًا ما تعرَّضَ لإزاحة، ليست بالضرورة صغيرة، من موضع ابتدائي 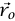 إلى موضع نهائي
إلى موضع نهائي  . نحدّد أيضًا المسار الذي سلكه الجسيم وليس بالضرورة أن يكون خطا مستقيما. من الناحية المفاهيمية، نستطيع تقسيم المسار إلى سلسلة من الإزاحات الصغيرة جدًّا
. نحدّد أيضًا المسار الذي سلكه الجسيم وليس بالضرورة أن يكون خطا مستقيما. من الناحية المفاهيمية، نستطيع تقسيم المسار إلى سلسلة من الإزاحات الصغيرة جدًّا  كلٌّ منها خط مستقيم (انظر شكل 5–2). لتكن
كلٌّ منها خط مستقيم (انظر شكل 5–2). لتكن  هي لقوة المؤثرة على الجسيم عندما يتعرّض للإزاحة
هي لقوة المؤثرة على الجسيم عندما يتعرّض للإزاحة  . الشغل المبذول على الجسيم أثناء هذه الخطوة القصيرة هو
. الشغل المبذول على الجسيم أثناء هذه الخطوة القصيرة هو  .
. والشغل الكلي المبذول على الجسيم أثناء حركته من
والشغل الكلي المبذول على الجسيم أثناء حركته من 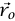 إلى
إلى  ما يعرف بالمعادلة:
ما يعرف بالمعادلة:
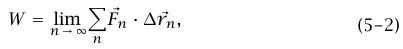
حيث ”lim" تعني أننا مهتمون بالقيمة الحدِّيَّة أو النهاية للمجموع كلما أصبح طول الخطوات أصغر فأصغر، ويصبح عدد الحدود في المجموع أكبر فأكبر تباعًا.
الحد أو النهاية التي عرفناها بوضوح هي تعميم لمفهوم التكامل، وتُمثَّل عمومًا بالرمز:

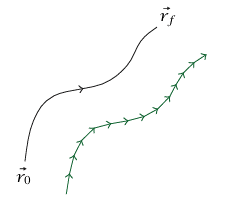
شكل 5–2: تقسيم المسار.
الذي يشير عادةً إلى «التكامل الخطي للقوة  من
من 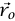 إلى
إلى  .» وينتج أن:
.» وينتج أن:

قد يجد الطالب أنه من المفيد والأفضل أن يتذكر المعادلة (2–5) بدلا من المعادلة (4–5) لأن المعادلة (2–5) يمكن تصورها بسهولة. واعتمادًا على طبيعة القوة  ، يمكن، أو لا يمكن أن يكون للطرف الأيمن من المعادلة (4–5) نفس القيمة لكل المسارات بين نقطتين طرفيتين محدَّدتين
، يمكن، أو لا يمكن أن يكون للطرف الأيمن من المعادلة (4–5) نفس القيمة لكل المسارات بين نقطتين طرفيتين محدَّدتين 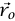 و
و . في الحالة الخاصة، حيث يكون للقوة
. في الحالة الخاصة، حيث يكون للقوة  نفس القيمة عند جميع نقاط المسار، يكون لدينا (باستخدام خاصية التوزيع لحاصل الضرب القياسي):
نفس القيمة عند جميع نقاط المسار، يكون لدينا (باستخدام خاصية التوزيع لحاصل الضرب القياسي):

مثال 5–1 (الشغل المبذول بواسطة الجاذبية). احسب الشغل المبذول بواسطة الجاذبية على جسيم يتحرك من موضع ابتدائي 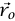 إلى موضع نهائي
إلى موضع نهائي  . من المفترض أن
. من المفترض أن 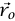 و
و قريبان بدرجة كافية من سطح الأرض، وكل منهما قريب من الآخر، بحيث تكون قوة الجاذبية التثاقلية ثابتة؛ أي إن
قريبان بدرجة كافية من سطح الأرض، وكل منهما قريب من الآخر، بحيث تكون قوة الجاذبية التثاقلية ثابتة؛ أي إن 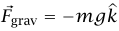 .
.
يمكننا كتابة  وكتابة نفس الشيء للموضع
وكتابة نفس الشيء للموضع  . باستخدام المعادلة (5–5) و
. باستخدام المعادلة (5–5) و 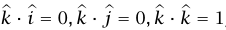 نجد أن:
نجد أن:

لاحظ أن الشغل الذي تبذله الجاذبية يعتمد فقط على الموضعين الابتدائي والنهائي، ولا يعتمد على مسار معين يسلكه الجسيم بين هذين الموضعين. هذا صحيح حتى عندما نعتبر تغير مقدار واتجاه قوة الجاذبية التثاقلية عندما يتحرك الجسيم خلال مسافات كبيرة. الشغل الذي تبذله الجاذبية هو نفسه لكل المسارات بين نقطتين معينتين، ولكنه عموما لا يُعطى بالمعادلة (6–5) الإشارة التي يدخل بها كلٌّ من z0 و zf في المعادلة (6–5) يمكن تذكَّرها بملاحظة أن الجاذبية تبذل شغلًا موجبًا على الجسيم الذي يتحرك لأسفل (تكون القوة موازية للإزاحة)، وتبذل شغلًا سالبًا على الجسيم الذي يتحرك لأعلى.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















