يمكن حل المعادلة التفاضلية (معادلة (2–6)) بدون حساب التفاضل باستخدام إنشاء هندسي بسيط. ولأن هدفنا في هذا القسم هو الإحجام عن استخدام حساب التفاضل، فإننا نستبدل a_x بدلا من dt²/d²x (قد يبدو الرمز السفلي × غير ضروري لكنه سيساعد في تجنب الالتباس اللاحق) مشكلتنا هي إيجاد حركة جسيم على المحور x، بمعلومية أن العجلة تتناسب مع سالب الإزاحة؛ أي إن:

نتذكر أن الجسيم المتحرك في دائرة نصف قطرها r بمقدار سرعة ثابت v يكون متجه عجلته:

حيث 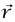 هو المتجه من مركز الدائرة إلى الموضع اللحظي للجسيم و هو متجه الوحدة في نفس اتجاه 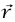. إذا كانت الدائرة في المستوى x–y، فإن 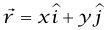وينتج من المعادلة (16–6) أن:

دعنا نختار v وr بحيث تكون النسبة r/v مساوية لـ ω في المعادلة (15–6)، ولذلك تصبح المعادلة (17–6) مماثلة للمعادلة (15–6). وبما أن v/r هي السرعة الزاوية (وهي الإزاحة الزاوية لوحدة الزمن، مقيسة بوحدة التقدير الدائري لكل ثانية) للجسيم المتحرك حول الدائرة، نرى أن السرعة الزاوية تساوي ω.

ليكن P الموضع اللحظي لجسيمنا على الدائرة، ودعنا نسقط خطًا عموديا من P على المحور x، ليقطع المحور x عند النقطة Q. إذن بما أن عجلة Q على المحور x هي a_x، نرى أن حركة Q تحقق المعادلة (15–6). بإيجاز، إذا أُسقطت الحركة الدائرية المنتظمة على خط، تكون الحركة الخطية الناتجة حركة توافقية بسيطة. (الادعاء بأن هذه المناقشة لا تعتمد على حساب التفاضل ليس صحيحًا تمامًا؛ لأن اشتقاق المعادلة (6–16)، المسؤولة عن إنشاء الفرق بين متجهي السرعة عند زمنين قريبين أحدهما على الآخر من بعض والقسمة على الفارق الزمني، هو حساب تفاضل.) تسمى الدائرة دائرة المرجع، وهي بناء رياضياتي صرف.

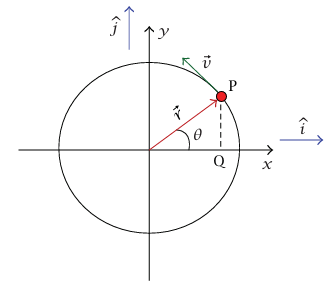
شكل 6–4: صياغة الحل البياني للحركة التوافقية البسيطة.

بالاختيار المناسب لنصف قطر دائرة المرجع والموضع الابتدائي P للجسيم على دائرة المرجع، يمكننا أن نجعل Q تأخذ أي موضع وسرعة ابتدائيين مرغوبين. الإحداثي x لـ P هو r cos θ؛ حيث θ الزاوية بين 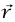 والمحور x (انظر الشكل 6–4). إذا كانت قيمة θ عند 0 = t هي δ– (هذا هو تعريف δ) ، وإذا كانت P تتحرك حول الدائرة في عكس اتجاه عقارب الساعة بسرعة زاوية ω؛ فإن δ –θ= ωt ؛ وبالتالي يكون:

سرعة النقطة P تكون في اتجاه المماس للدائرة ومقدارها rω = v. والمركبة × لسرعة P، وهي سرعة Q، تكون (انظر شكل 6–4):

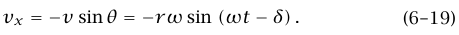
لاحظ أنه كان باستطاعتنا الحصول على المعادلة (19–6) عن طريق تفاضل المعادلة (18–6) بالنسبة إلى الزمن، ولكننا نستخدم الهندسة في هذا القسم وليس حساب التفاضل.

بوضع 0 = t في المعادلتين (18–6) و(19–6) نحصل على x₀ = r cos δ وv₀ = r ω sin δ (استخدمنا sin (–δ) = –sin (δ), cos (–δ) = cos δ )؛ حيث x₀ وv₀ الإزاحة والسرعة الابتدائيتان؛ وبالتالي فإن

من المفيد تعليميًّا رسم المنحنى البياني السليم نوعيًّا لكل من x، وv_x، وa_x مقابل t عن طريق تخيل حركة النقطة P على دائرة المرجع. لا بد أن تقارن رسوماتك البيانية مع المعادلتين (18–6) و (19–6) اجعل 0 = t في اللحظة التي عندها x = x_max؛ أي إن θ = 0 ينبغي أن يكون واضحًا أن مقدار السرعة يكون صفرا عند
x = ± x_max ويكون مقدار السرعة أكبر ما يمكن عند 0 = x.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

امثلة عن الاتزان الاستاتيكي للأجسام الممتدة

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل

تصادمات مرنة ثنائية البعد