مثال 7–1 الاتزان الاستاتيكي لقضيب متزن). قضيب منتظم وزنه W وطوله L يستند على دعامتين؛ إحداهما عند نهاية الطرف الأيسر والأخرى على بعد 3/4 L من نهاية الطرف الأيسر. أوجد القوة التي يؤثر بها كل من الدعامتين على القضيب.

الحل. نضع متجهات الوحدة: 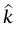 الذي يشير رأسيًا لأعلى،  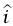الذي يشير نحو اليمين،  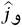إلى داخل الورقة كما هو مبين في شكل 7–5 القوى المؤثرة على القضيب هي المؤثرة عند نهاية الطرف الأيسر، و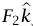المؤثرة على بعد3/4L  من نهاية الطرف الأيسر، وقوة الجاذبية  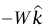التي يمكن اعتبارها مؤثرة عند نقطة المنتصف. وبما أن القوى الكلية على القضيب صفر، فإن:

لا بد أن يكون العزم الكلي حول أي نقطة أصل صفرًا. إذا أخذنا نقطة الأصل عند نهاية الطرف الأيسر للقضيب، فإن القوة 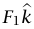 لا تساهم بأي عزم ونحصل على:

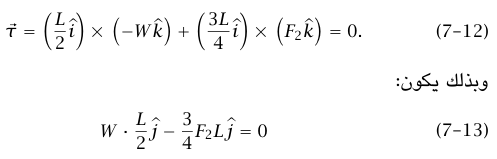
وبالتالي فإن F₂ = 2/3W. باستخدام المعادلة (11–7) نجد أن F₁ = 1/3W. كان في إمكاننا أيضًا أخذ العزوم حول نقطة أصل أخرى، مثلا، الدعامة الأخرى. نجد في هذه الحالة:

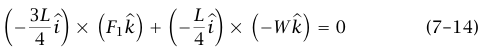
لنصل إلى أن 3/F₁ = W وبذلك نرى أنه يمكن حل المسألة بكتابة معادلة قوة واحدة ومعادلة عزم واحدة، أو بكتابة معادلتي عزم حول نقطتي أصل.

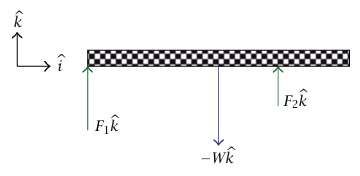
شكل 7–5: القوى المؤثرة على قضيب متزن عند نقطتين.

إذا كانت القوة الكلية على نظام ما صفرًا، وإذا كان العزم حول نقطة أصل معينة صفرًا، فينتج من ذلك أن العزم حول أي نقطة أصل أخرى يكون صفرًا. لرؤية ذلك، لتكن O وO' نقطتي أصل، و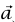 هو المتجه الواصل من O' إلى O. افترض أن القوة

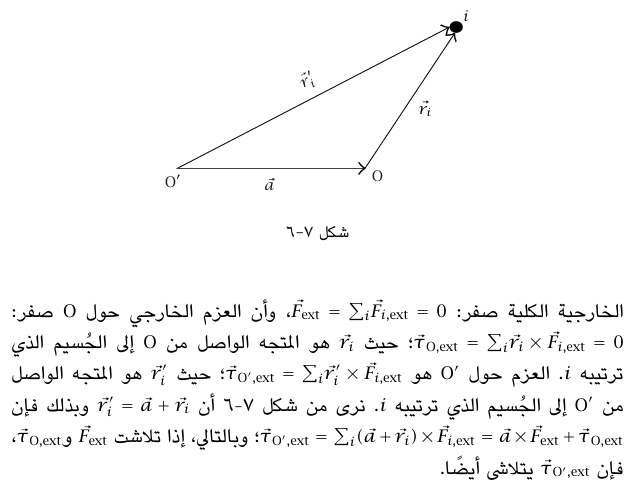
هذا يعني أن المعلومات عن أي نظام بعينه محتواة داخل معادلة القوة بالإضافة إلى معادلة العزم حول نقطة أصل واحدة. وأي معادلات إضافية يُحصل عليها بأخذ العزم حول نقط أصل أخرى ستكون نتائج جبرية لمعادلة القوة ومعادلة العزم الأولى. بيَّنَّا أن تلاشي القوة والعزم الخارجيين الكليين هما شرطان ضروريان لاتزان نظام ما. ولكن هل سيكون أيضًا هذان الشرطان كافيين للاتزان؟ إذا لم يكن النظام جسمًا جاسئًا فبالتأكيد ستكون الإجابة «لا»، وذلك كما يظهر من اعتبار العديد من الأمثلة البسيطة، مثل ذلك الموضح في شكل 7–7 كل من القوة والعزم الكليين يساوي صفرا، وبالإضافة لذلك سوف يتحرك الجسيمان أحدهما نحو الآخر بعجلة تزايدية. إذا كان النظام جسمًا جاسئًا، وكانت جميع جسيمات النظام ساكنة عند لحظة ما، فيمكن أن نبين أن جميع جسيمات النظام سوف تظل ساكنة إذا تلاشى كل من القوة والعزم الخارجيين الكليين. يتضمن البرهان، الذي سوف يقدم في الفصل التالي، تحليلا للحركات الممكنة لجسم جاسئ (التي تكون محدودة على نحو هائل بالمقارنة بحركات مجموعة اختيارية من الجسيمات).

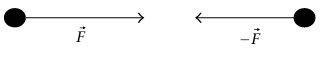
شكل 7–7

جميع الأمثلة الاستاتيكية التي سوف نناقشها ثنائية الأبعاد؛ أي إن جميع الجسيمات وجميع القوى تكون في مستوى (سوف نجعله مستوى الصفحة). طبقًا لذلك، تكون جميع العزوم متعامدة على هذا المستوى وتتناسب (كما يُشار في مثال 7–1) مع 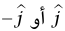. العزم المتناسب مع  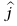يتجه إلى داخل الصفحة ويُسمى غالبًا «عزم مع عقارب الساعة»، والعزم المتناسب مع 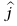– يتجه إلى خارج الصفحة ويُسمى غالبًا «عزم ضد عقارب الساعة»؛ وبذلك يمكننا حذف جميع المتجهات في معادلة العزم، بشرط أن نتذكر وضع إشارات معكوسة للعزوم التي مع وضد عقارب الساعة.

في شكل 7–5 تصنع القوة 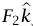عزمًا ضد عقارب الساعة حول نهاية الطرف الأيسر للقضيب. وتصنع القوة 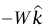عزمًا مع عقارب الساعة. لاحظ أنه في شكل 7–5 «تحاول» القوة  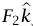إدارة القضيب في اتجاه ضد عقارب الساعة حول نهاية طرفه الأيسر، بينما تحاول» القوة  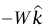إدارة القضيب في اتجاه مع عقارب الساعة حول نهاية طرفه الأيسر. إذا أخذنا نقطة الأصل عند نهاية الطرف الأيمن للقضيب، فإن كلَّا من  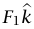و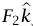 تصنعان عزمًا مع عقارب الساعة وتصنع  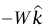عزمًا ضد عقارب الساعة. على الطلاب الذين يجدون صعوبة مع الإشارات حساب حاصلات الضرب المتجهية ببساطة.

مثال 7–2 (اتزان استاتيكي لقضيب معلق). قضيب منتظم AB، وزنه W، مثبت إلى حائط باستخدام مفصل أملس عند A وأبقي عليه في وضع أفقي باستخدام سلك CB عديم الوزن يصنع زاوية θ مع الأفقي. احسب الشد في السلك والمركبتين الرأسية والأفقية للقوة التي يؤثر بها الحائط على القضيب.

الحل. نعرض في شكل 7–9 جميع القوى المؤثرة على القضيب. V وH هما مقدارا القوتين الرأسية والأفقية اللتين يؤثر بهما الحائط عند A من المفترض أن تكون هاتان القوتان في الاتجاهين الموضحين بالسهمين. إذا اتضح أن V سالبة، فسوف نعلم من المعادلات أن القوة الرأسية التي يؤثر بها الحائط متجهة إلى أسفل وليس إلى أعلى، سوف تعني قيمة H السالبة أن الحائط يؤثر بقوة أفقية متجهة نحو اليسار.

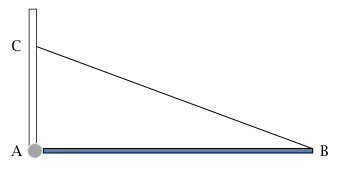
شكل 7–8: قضيب معلق عند حائط ومسنود من نهاية طرفه الآخر بوتر.

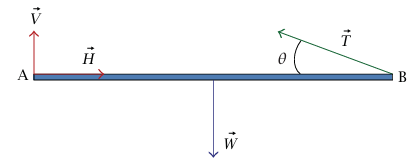
شكل 7–9: مخطط القوة للمثال 7–2.

لاحظ أن هناك ثلاثة مجاهيل (V, H, T) وثلاث معادلات تنص على شروط اتزان القضيب (مركبتان لمعادلة القوة ومعادلة عزم واحدة)؛ وبالتالي فإن المسألة محددة رياضيا. المعادلتان الأفقية والرأسية للقوة هما:

حيث L طول القضيب، وبذلك يكون T = W/(2 sin θ) وبالتعويض في المعادلة (15–7) نجد أن H = (w/2) cot θ وV = W/2. كان من الممكن إيجاد قيمة V مباشرة بأخذ العزوم حول B.

مثال 7–3 (الاتزان الاستاتيكي لقضيب معلق ومربوط). تكرس معظم المقررات التمهيدية القليل جدًّا من الوقت للاستاتيكا ونتيجة لذلك، فإن قلة قليلة من الطلاب تكتسب الأسلوب الملائم لحل مسائل كهذه المسألة، ويندر من بين هذه القلة من يستطيع حلها بكفاءة. غير أنه من المفضل أن يدرس الطالب هذا المثال الذي يوضح عددًا من النقاط المهمة.

الشكل الهندسي لهذا المثال مشابه لمثال 7–2، AB قضيب وزنه W، وCB قضيب وزنه W'، والوصلات عند A وB وC هي مفاصل ملساء. احسب القوتين الأفقية والرأسية اللتين يؤثر بهما الحائط عند A وعند C، والقوتين الأفقية والرأسية اللتين يؤثر بهما كل قضيب على الآخر عند B.

الحل. هناك عدة قوى مجهولة في هذه المسألة. سوف تصبح العمليات الجبرية سهلة بقدر كبير إذا حذفنا من البداية بعض المجاهيل باستخدام معادلات القوة وقانون نيوتن الثالث من المهم أيضًا إدراك أن هناك ثلاثة أنظمة مختلفة (القضيب AB، والقضيب CB، والنظام ABC المتكون من القضيبين) ويمكن كتابة معادلات القوة والعزم لها. [ومع ذلك، ليست كل المعادلات مستقلة جبريًا. إذا تلاشت القوة والعزم على أي اثنين من هذه الأنظمة، فإن القوة والعزم على النظام الثالث يتلاشيان أيضًا.]

عرضنا في شكل 7–10 جميع القوى الخارجية المؤثرة على ABC (تكون القوى عند الوصلة قوى داخلية في النظام ABC) نرمز إلى القوتين الأفقية والرأسية عند A بالرمزين 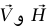، مع افتراض اتجاههما كما هو موضح بالسهمين. حينئذٍ يلزم تعيين القوتين الأفقية والرأسية عند C تلاشي القوتين الكليتين الأفقية والرأسية ABC. بالمثل، يبين شكل 7–11 القوى المؤثرة على AB (لاحظ أن القوى عند نهاية الطرف الأيمن هي القوى المؤثرة بواسطة القضيب CB على القضيب AB). يبين شكل 7–12 القوى المؤثرة على القضيب CB؛ وبالتالي فإنه باستخدام معادلات القوة اختزلنا عدد المجاهيل إلى مجهولين.

أسهل طريقة نستطيع بها تعيين 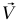 هي بأخذ العزوم على AB حول نقطة الأصل B، لنحصل على 0 = 2/L) VL – WL = طول (AB وبهذا تكون 2/V = W.

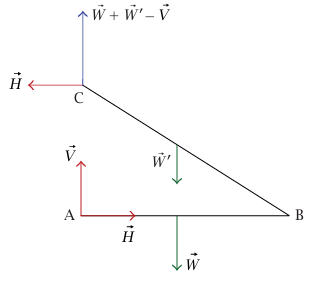
شكل 7–10: مخطط القوة للنظام المركب ABC لمثال 7–3.

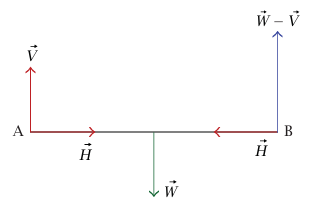
شكل 7–11: مخطط القوة للقضيب AB في مثال 7–3.

وإحدى الطرق السهلة لحساب  هي أخذ العزوم على ABC حول نقطة الأصل A (شكل 7–10)، لنحصل على 0 = θ WL/2 + W'L/2 – HL tan، وبهذا تكون H = (1/2) (W + W') cot θ. يمكن للمرء، بالطبع، كتابة معادلات عزم أخرى تؤدي لنفس قيمتي H وV. بإدخال قيمتي H وV في الأشكال من 7–10 إلى 7–12 نحصل على القوى.

أحد الأخطاء الشائعة هي افتراض أن القوة التي يؤثر بها القضيب CB على الحائط متوازية مع القضيب CB. لو كان هذا صحيحًا لكانت القوة التي يؤثر بها الحائط على CB متوازية أو متوازية (بالعكس) هي أيضًا مع CB ولصنعت عزمًا حول B؛ وبالتالي فإن العزم الوحيد على CB حول نقطة الأصل B سيكون العزم الناتج من 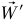 ولن يتمكن القضيب من أن يكون في حالة اتزان إلا إذا كانت 0 = 'W، في هذه الحالة تكون القوة التي يؤثر بها CB على الحائط متوازية مع CB).

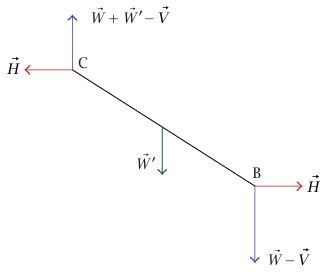
شكل 7–12: مخطط القوة للقضيب CB في مثال 7–3.

من المهم أيضًا فهم ما يعنيه «مفصل أملس»، ولماذا نفترض عادة أن الوصلة مثبتة بمفصل أملس. نفترض أن القضبان متصلة بعضها ببعض، وبسنادات على الحائط، بواسطة مسامير عمودية على مستوى الصفحة وتمر خلال ثقوب دائرية في القضبان (انظر الأشكال من 7–13 إلى 7–15). من المفترض أن سطح التماس بين المسمار والثقب مشحم جيدًا بحيث تكون القوى الوحيدة التي تؤثر عند ذلك السطح عمودية على السطح؛ وبالتالي إذا جعلنا مركز الثقب هو نقطة الأصل، فإننا نرى أن المسمار لا يؤثر بمحصلة عزم على القضيب (لكنه يؤثر غالبًا بمحصلة قوة). إذا ثبت القضيب بسنادة حائط بواسطة مفصل صدئ بدرجة كافية (شكل 7–15)، فيمكن أن يظل القضيب في وضع أفقي دون أي دعم إضافي. إذا جعلنا نقطة الأصل عند مركز الثقب، فإن الوزن W يصنع عزمًا على القضيب مع عقارب الساعة؛ رغم ذلك، تصنع المركبة المماسية للقوة التي يؤثر بها المسمار على سطح الثقب عزمًا ضد عقارب الساعة له نفس مقدار عزم الجاذبية (إذا كان المفصل صدئًا بدرجة كافية)؛ وبالتالي يكون القضيب في حالة اتزان.

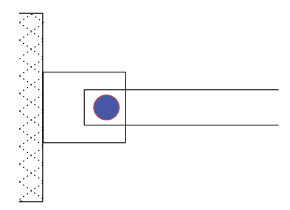
شكل 7–13: مفصل أملس.

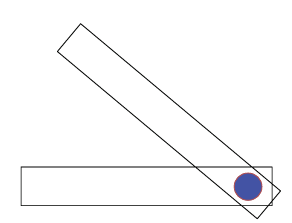
شكل 7–14: مفصل واصل بين قضيبين بزاوية بينهما.

يوضح هذا التحليل أهمية عدم المبالغة في جعل الموقف مثاليا. إذا اعتبرنا القضيب جسما أحادي البعد بمعنى الكلمة، بحيث يكون للمسمار والثقب نصف قطر يساوي صفرا، فلن نستطيع فهم كيف يمكن أن يصنع المسمار الصدئ عزمًا حول مركز الثقب.

إحدى الحالات وثيقة الصلة، وذات أهمية في التصميم المعماري والهندسة، هي لقضيب أفقي، أُدخلت إحدى نهايتيه في ثقب في الحائط.

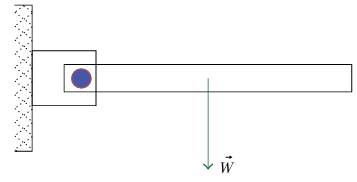
شكل 7–15: قضيب وزنه W مثبت إلى حائط بواسطة مفصل صدئ.

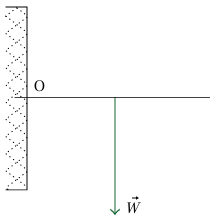
شكل 7–16: قضيب في ثقب في حائط.

إذا عرفنا نظامنا بأنه جزء القضيب خارج الحائط، وإذا أخذنا نقطة الأصل O النقطة التي يدخل عندها القضيب في الحائط (شكل 7–16)، فيتضح إذن أن العزم الوحيد على النظام هو عزم الجاذبية. مرة أخرى، لا بد أن ندرك أن للقضيب سمكا محدودًا. في الواقع، يتدلى الجزء البارز من القضيب قليلا بحيث يُطيل الجزء العلوي من القضيب بقدر بسيط (في الشد) وينضغط الجزء السفلي بقدر بسيط. قسمنا القضيب في شكل 7–17 إلى جزء I خارج الحائط وجزء II داخل الحائط بواسطة مستوى تخيلي. يصور شكل 7–17 تخطيطا للقوى التي يؤثر بها II على I خلال المستوى المقسم. في الجزء العلوي من القضيب، يؤثر II بقوة سحب على I نحو اليسار، وفي الجزء السفلي للقضيب يؤثر II بقوة دفع على I نحو اليمين.

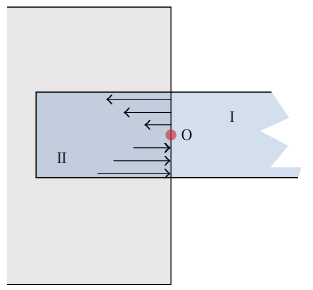
شكل 7–17

إذا أخذنا نقطة الأصل عند نقطة O منتصف المستوى المقسّم، فمن الواضح أن نظام القوى الموضح في شكل 17–7 يصنع عزمًا ضد عقارب الساعة يلغي عزم الجاذبية مع عقارب الساعة. الأكثر من ذلك، II يؤثر بقوة رأسية (قص) على I تسمح بتحقيق معادلة القوة. تحليل القوى الداخلية في القضبان والتشوه الصغير المصاحب لتلك القوى، هو خارج نطاق هذه المناقشة.

مثال 7–4 (سلم يتكئ على جدار أملس). سلم منتظم يقف مستندًا بنهاية طرفه العلوي على حائط أملس ويستند طرفه السفلي على أرضية خشنة (معامل الاحتكاك الاستاتيكي μ_s). يميل السلم بزاوية θ على الأفقي احسب القوتين الرأسية والأفقية التي تؤثر بهما الأرضية، واحسب أقل زاوية θ يمكن عندها أن يقف السلم دون أن ينزلق.

الحل. يبين شكل 7–19 القوى المؤثرة على السلم. يمكن للحائط، لكونه أملس، أن يؤثر فقط بقوة أفقية 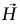 متجهة نحو اليمين. لكي تتلاشى القوة الكلية على السلم، لا بد أن تؤثر الأرضية بقوة مقدارها H متجهة نحو اليسار وقوة رأسية تساوي وزن السلم W.

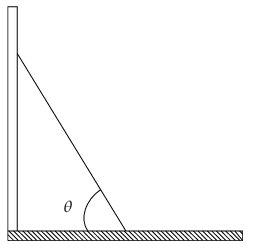
شكل 7–18: سلم يتكئ على جدار أملس في مثال 7–4.

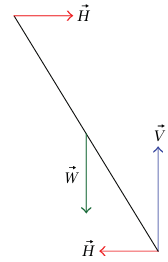
شكل 7–19: مخطط القوة لسلم يتكئ على جدار أملس.

بأخذ العزوم حول نهاية الطرف السفلي للسلم، نجد أن:

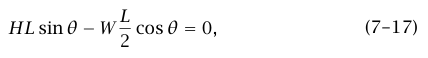
حيث L طول السلم؛ وبذلك تكون H = (W/2) cot θ لكي لا ينزلق السلم لا بد أن يكون H/W ≤ μ_s؛ أي إن (1/2) cot θ ≤ μ_s؛ وبالتالي فإن θ_min = cot^–1 (2μ_s).

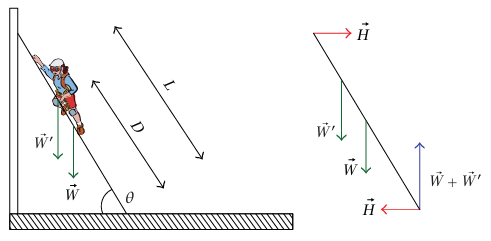
شكل 7–20: تسلق سلم يتكئ على جدار أملس في مثال 7–5.

مثال 7–5 (تسلق سلم يتكئ على جدار أملس). نبين في شكل 7–20 سيدة وزنها 'W عند مسافة D من أسفل سلم طوله L ووزنه W يميل فوق الأفقي بزاوية °60.0. ليكن W = 222 newtons وL = 6.10 meters معامل الاحتكاك الاستاتيكي بين السلم والأرضية هو μ_s.

(أ) إذا كان 0.600 = μ_s، فاحسب وزن أثقل شخص يستطيع التسلق إلى قمة السلم دون أن يتسبب في انزلاقه. أجب على نفس السؤال إذا كان 0.500 = μ_s.

(ب) إذا كان 0.500 = μ_s، فما أقصى ارتفاع على السلم يستطيع أن يصعد إليه شخص وزنه 1110 نیوتن (W') قبل أن ينزلق السلم؟

الحل. يبين مخطط القوة في شكل 7–20 القوى المؤثرة على السلم (من المفترض أن وزن السيدة الكلي متزن حول ركبتها وهي تتكئ على السلم، وأن الركبة تبعد مسافة D عن أسفل السلم) بأخذ العزوم على السلم حول نهاية الطرف السفلي، نجد أن: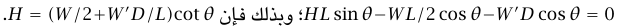 ولكي لا ينزلق السلم، لا بد أن يكون لدينا H/(W+W') ≤ μ_s؛ أي إن:

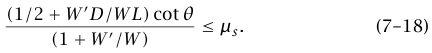
لاحظ أن الطرف الأيسر من المعادلة (18–7) يزيد بزيادة D؛ وبالتالي، إذا تحققت المعادلة (18–7) عند D = L ، فإنها تتحقق أيضًا عند D < L؛ وبذلك فإن السيدة تستطيع الوصول إلى قمة السلم إذا كان:

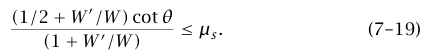
شكل 7–21 عبارة عن رسم بياني للمقدار (1/2 + W'/W) / (1 + W'/W) كدالة في W'/W. الرسم البياني دالة متزايدة في W'/W تقترب من القيمة التقرُّبية 1 كلما كان ∞ → W'/W. وطبقًا لذلك، إذا كان cot θ ≤ μ_s، فإن أي شخص (مهما كان وزنه) يستطيع التسلق إلى القمة دون أن يتسبب في انزلاق السلم. في هذه المسألة θ = 60^o وcot θ = .577؛ وبالتالي إذا كان 0.6 = μ_s، فإن أي شخص يمكنه الوصول للقمة. وإذا كان 0.5 = μ_s، فإننا نوجد وزن أثقل شخص يمكنه الوصول للقمة بوضع الطرف الأيسر من المعادلة (719) مساويًا لـ 0.5 يؤدي هذا إلى أن 2.73 = W' / W = (μ_s – 1/2cot θ) / (cot θ – μ_s) ؛ وبالتالي فإن W' = 606 newtons أو حوالي 136 رطلا. إذا كان W' = 1110 newtons، فإن السلم سوف ينزلق قبل أن يصل الشخص للقمة. بوضع الطرف الأيسر من المعادلة (18–7) مساويًا لـ 0.5 وبإدخال 5 = W'/W نجد أن (1/2 + 5D/L) (.577) / 6 = .5، وهو ما يؤدي إلى أن 940. = D/L؛ وبالتالي فإن D = 5.73 متر أو حوالي 18.8 قدمًا بالنسبة لسلم طوله حوالي 20 قدمًا.

قبل ترك موضوع الاستاتيكا، ينبغي لنا أن ندرك أننا قصرنا اهتمامنا على المواقف المحددة رياضيا؛ أي المواقف التي يمكن فيها تعيين جميع القوى بواسطة معادلات القوة والعزم دون الحاجة إلى معلومات إضافية تفصيلية عن النظام. الأمثلة التالية، غير المحددة استاتيكيا، توضح حقيقة أن معادلات القوة والعزم ليست كافية دائمًا للإجابة على جميع الأسئلة.

(أ) سلم يتكئ على حائط خشن وقاعدته على أرضية خشنة. هناك أربع قوى مجهولة (قوة رأسية وأخرى أفقية عند كل طرف من طرفي السلم) وثلاث معادلات فقط (معادلة عزم ومعادلة قوة أفقية ومعادلة قوة رأسية).

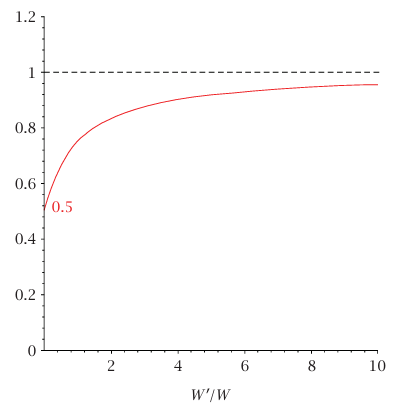
شكل 7–21: رسم بياني للمقدار (1/2 + W'/W) / (1 + W'/W) كدالة في W'/W في المثال 7–5.

(ب) قضيب أفقي مدعوم عند ثلاث نقاط هناك ثلاث قوى مجهولة ومعادلتان (معادلة قوة ومعادلة عزم).

(جـ) علامة معلقة على حائط بواسطة مفصلين أملسين عند نقطتين (انظر شكل 7–22). هناك أربع قوى مجهولة (قوتان عند كل مفصل) وثلاث معادلات.

الطبيعة، بالطبع، ليست غير محددة. لا يمكن في أي من هذه الأمثلة معالجة عدم التحديد الظاهر إلا بمعرفة شيء ما عن خواص المرونة للأجسام قيد الاعتبار، فجميع الأجسام تخضع لتشوهات صغيرة عند تعرضها لقوى. نحتاج في هذه الحالات إلى معرفة العلاقة بين التشوهات والقوى بهذه المعلومات إلى جانب معادلات القوة والعزم، يمكن تعيين جميع القوى.

شكل 7–22: علامة معلقة في حائط بواسطة مفصلين أملسين.

مواضيع ذات صلة

أنظمة لأكثر من جسيم واحد

كمية التحرك الزاوية والقوة المركزية

الحركة الدورانية

الاتزان الاستاتيكي للأجسام الممتدة

تعريف العزم

تذبذبات صغيرة لبندول

اعتبارات الطاقة في الحركة التوافقية البسيطة

الحل الهندسي للمعادلة التفاضلية للحركة التوافقية البسيطة، دائرة المرجع

الحل باستخدام حساب التفاضل والتكامل

قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة

القدرة ووحدات الشغل

تصادمات مرنة ثنائية البعد