
الاتزان الاستاتيكي للأجسام الممتدة
 المؤلف:
مايكل كوهين
المؤلف:
مايكل كوهين
 المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
 الجزء والصفحة:
ص 203 – ص 206
الجزء والصفحة:
ص 203 – ص 206
 2024-09-30
2024-09-30
 1464
1464
دعنا نعتبر نظامًا ما (أي مجموعة من الجسيمات) في حالة اتزان (أي إن كل جسيم يكون في حالة اتزان). ونرقم الجسيمات باستخدام الدليل i. القوة الكلية على كل جسيم تساوي صفرًا.

علاوة على ذلك، إذا اخترنا نقطة أصل O وقمنا بضرب طرفي المعادلة (2–7) متجهيًّا في 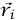 (المتجه الواصل من O إلى موضع الجسيم الذي ترتيبه i)، نجد أن:
(المتجه الواصل من O إلى موضع الجسيم الذي ترتيبه i)، نجد أن:

نتذكر أنه إذا جمعنا المعادلات (2–7) لجميع قيم i، فإن القوى الداخلية يلغي بعضها بعضًا كنتيجة لقانون نيوتن الثالث ونحصل على:

حيث 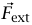 هي القوة الكلية الخارجية المؤثرة على النظام. هل نستطيع أيضًا القول بأن القوى الداخلية لا ينتج عنها محصلة للعزم مؤثرة على النظام؟
هي القوة الكلية الخارجية المؤثرة على النظام. هل نستطيع أيضًا القول بأن القوى الداخلية لا ينتج عنها محصلة للعزم مؤثرة على النظام؟

لاختبار هذا السؤال نحلل 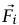 إلى جزأين خارجي وداخلي:
إلى جزأين خارجي وداخلي:

ويمكن دمج ذلك (باستخدام قانون نيوتن الثالث  ) ليعطي
) ليعطي 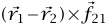 . يتلاشى حاصل الضرب المتجهين هذا إذا كانت
. يتلاشى حاصل الضرب المتجهين هذا إذا كانت 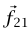 متوازية إما مع اتجاه أو عكس اتجاه
متوازية إما مع اتجاه أو عكس اتجاه  لكن
لكن  هو متجه واصل من الجسيم رقم 2 إلى رقم 1؛ وبالتالي إذا كانت القوة بين أي جسيمين متوازية إما مع اتجاه أو عكس اتجاه الخط الواصل بين الجسيمين، فإن الضرب المتجهين سوف يتلاشى ولن تساهم القوى الداخلية في العزم الكلي. القوى التي تؤثر على طول الخط الواصل بين الجسيمين تسمى قوى مركزية؛ من الأمثلة المألوفة قوة الجاذبية والقوة الكهروستاتيكية (اللتان لهما نفس الصورة الرياضياتية). بعض القوى في الطبيعة ليست قوى مركزية، ومن أكثر الأمثلة المألوفة القوى المغناطيسية حتى في هذه الحالة، رغم ذلك، يمكن من خلال حجة أكثر تفصيلا إظهار أن القوى الداخلية لا تساهم في العزم الكلي لو لم يكن هذا صحيحًا لبدأ نظام ما معزول، تحت ظروف معينة، في الدوران أسرع فأسرع ولتمكن من بذل شغل دون أي طاقة داخلة.
هو متجه واصل من الجسيم رقم 2 إلى رقم 1؛ وبالتالي إذا كانت القوة بين أي جسيمين متوازية إما مع اتجاه أو عكس اتجاه الخط الواصل بين الجسيمين، فإن الضرب المتجهين سوف يتلاشى ولن تساهم القوى الداخلية في العزم الكلي. القوى التي تؤثر على طول الخط الواصل بين الجسيمين تسمى قوى مركزية؛ من الأمثلة المألوفة قوة الجاذبية والقوة الكهروستاتيكية (اللتان لهما نفس الصورة الرياضياتية). بعض القوى في الطبيعة ليست قوى مركزية، ومن أكثر الأمثلة المألوفة القوى المغناطيسية حتى في هذه الحالة، رغم ذلك، يمكن من خلال حجة أكثر تفصيلا إظهار أن القوى الداخلية لا تساهم في العزم الكلي لو لم يكن هذا صحيحًا لبدأ نظام ما معزول، تحت ظروف معينة، في الدوران أسرع فأسرع ولتمكن من بذل شغل دون أي طاقة داخلة.
طبقًا لذلك، نؤكد (رغم أن الإثبات العام تمامًا خارج نطاق هذه المناقشة) على أنه، إذا كان نظام ما في حالة اتزان فإن القوى الداخلية لا تساهم في العزم الكلي؛ وبالتالي:
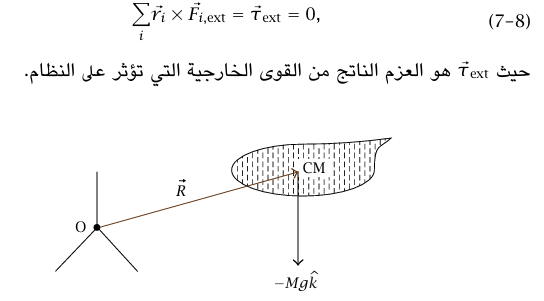
شكل 7–4: عزم حول نقطة الأصل ناتج من الجاذبية المؤثرة على جسم O.
في معظم الأمثلة التي سوف نعتبرها هنا تكون قوة الجاذبية واحدة من القوى الخارجية المؤثرة على نظام ما تؤثر هذه القوة على كل جسيم في النظام؛ حيث إن الجسيمات المختلفة على مسافات  مختلفة من نقطة الأصل O. رغم ذلك، هناك نظرية هامة تجعل من حساب العزم الناتج بواسطة الجاذبية أمرًا سهلًا. (نفترض هنا أن منطقة الاهتمام صغيرة بقدر كافٍ بحيث يكون مقدار واتجاه قوة الجاذبية لوحدة الكتلة متماثلين لجميع الجسيمات في النظام تحت الدراسة.)
مختلفة من نقطة الأصل O. رغم ذلك، هناك نظرية هامة تجعل من حساب العزم الناتج بواسطة الجاذبية أمرًا سهلًا. (نفترض هنا أن منطقة الاهتمام صغيرة بقدر كافٍ بحيث يكون مقدار واتجاه قوة الجاذبية لوحدة الكتلة متماثلين لجميع الجسيمات في النظام تحت الدراسة.)
نظرية. من أجل حساب العزوم، يمكن اعتبار قوة الجاذبية الكلية على نظام ما أنها تؤثر على مركز الكتلة. (كما هو مبين في شكل 7–4 يكون عزم الجاذبية على النظام هو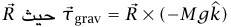 المتجه الواصل من نقطة الأصل إلى مركز كتلة النظام، وM الكتلة الكلية، و
المتجه الواصل من نقطة الأصل إلى مركز كتلة النظام، وM الكتلة الكلية، و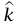 متجه وحدة يشير رأسيًا لأعلى.)
متجه وحدة يشير رأسيًا لأعلى.)
ينتج البرهان مباشرة من تعريف مركز الكتلة:
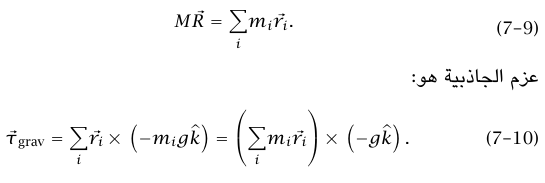
بإدخال المعادلة (79) في المعادلة (1) نحصل على 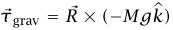 وهي النتيجة المطلوبة.
وهي النتيجة المطلوبة.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


