x

هدف البحث
بحث في العناوين
بحث في اسماء الكتب
بحث في اسماء المؤلفين

اختر القسم
موافق

تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
قانون هوك والمعادلة التفاضلية للحركة التوافقية البسيطة
المؤلف:
مايكل كوهين
المصدر:
الميكانيكا الكلاسيكية مقدمة أساسية
الجزء والصفحة:
ص 181 – ص 183
2024-09-29
170
حركة جسيم تحت تأثير قوة يتناسب مقدارها مع بعد الجسيم عن موضع اتزانه واتجاهها دائمًا نحو موضع الاتزان تُسمى حركة توافقية بسيطة. دعنا نعتبر، مثلًا، جُسيمًا متحركا في بعد واحد على سطح أفقي أملس. وكان زنبرك ما مربوطا بالجسيم ونهايته الأخرى مربوطة في حائط كما في شكل 6–1.
ليكن طول الاتزان للزنبرك L، والطول الفعلي للزنبرك عند لحظة معينة L + x. من المفترض أنه في حالة الاتزان تكون ملفات الزنبرك مفتوحة جزئيا بحيث يمكن أن تكون x إما موجبة أو سالبة. إذا كانت x موجبة فإن الزنبرك يؤثر بقوة نحو اليسار، وإذا كانت x سالبة فإن الزنبرك يؤثر بقوة نحو اليمين الزنبرك المثالي يتبع قانون هوك، الذي ينص على أن مقدار القوة يتناسب مع مقدار x.
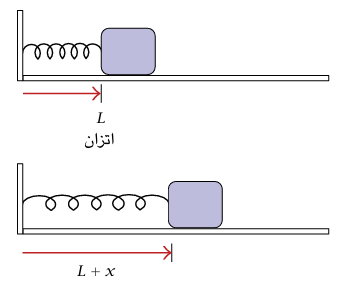
شكل 6–1: تعريف الاتزان في الحركة التوافقية البسيطة.
إذا استخدمنا متجه وحدة 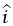 يشير نحو الاتجاه الذي يبتعد عن الحائط، وكانت القوة التي يؤثر بها الزنبرك على الجسيم
يشير نحو الاتجاه الذي يبتعد عن الحائط، وكانت القوة التي يؤثر بها الزنبرك على الجسيم 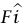 ، فإن التعبير الكمي لقانون هوك هو:
، فإن التعبير الكمي لقانون هوك هو:

حيث K ثابت يسمى ثابت الزنبرك. الإشارة السالبة في المعادلة (1–6) تؤكد أنه إذا كانت موجبة (سالبة)، فإن القوة تتجه نحو اليسار (اليمين).
قانون هوك (على عكس قوانين نيوتن) ليس قانوناً جوهرياً في الطبيعة، لكن معظم الزنبركات تتبع قانون هوك إذا كانت x صغيرة بقدر كافٍ، وتحيد جميع الزنبركات عن قانون هوك إذا تمددت أو انضغطت بقدر كبير جدًّا. سوف نفترض أن مقدار x صغير بما يكفي لأن يكون قانون هوك صالحًا. وحيث إن عجلة الجسيم 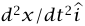 ، فإن قانون نيوتن الثاني يؤدي إلى:
، فإن قانون نيوتن الثاني يؤدي إلى:

المعادلة (2–6)، بالإضافة إلى الظروف الابتدائية (الموضع والسرعة الابتدائيين؛ أي مقداري x وdx/dt عند 0 = t)، تحدد على نحو تام الحركة التابعة رياضيا، مشكلتنا هي إيجاد دالة (t) تحقق المعادلة (2–6) (تسمى «معادلة تفاضلية») مبنية على قيمتين محددتين سالفًا لـ x وdx/dt عند 0 = t.
مثال 6–1 (استطراد رياضياتي). لتوضيح أن المعادلة (2–6) بالإضافة إلى قيمتين ابتدائيتين محددتين لـ x وdx/dt، تحدد على نحو فريد (x(t، يمكننا تخيل حل المعادلة (2–6) عدديًا. لتكن ε زيادة زمنية طفيفة جدًّا، ونجعل (من أجل تسهيل الترميز) vتشير إلى dx/dt وa تشير إلى d2x/dt2. وحيث إن (0)x و(0)v معلومتان، يمكننا حساب (ε)x و(ε)v باستخدام 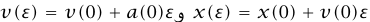 حيث تعطينا المعادلة (2–6) قيمة (0)a بمعرفة (0)x نعلم الآن قيمتي (ε)x و(ε)v و(باستخدام المعادلة .(2–6)) (ε)a نستطيع الآن حساب (ε2) x و(ε2)v و(ε2)a باستخدام
حيث تعطينا المعادلة (2–6) قيمة (0)a بمعرفة (0)x نعلم الآن قيمتي (ε)x و(ε)v و(باستخدام المعادلة .(2–6)) (ε)a نستطيع الآن حساب (ε2) x و(ε2)v و(ε2)a باستخدام 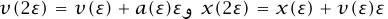 ؛ وبذلك نستطيع أن نتقدم بزيادات زمنية طفيفة. يمكن استخدام هذا الإجراء لحل معادلة تفاضلية من الدرجة الثانية (معادلة تكون المشتقة الأعلى درجة بها مشتقةً ثانيةً) عدديًا حتى عندما لا نستطيع إيجاد حل بدلالة دوال مألوفة.
؛ وبذلك نستطيع أن نتقدم بزيادات زمنية طفيفة. يمكن استخدام هذا الإجراء لحل معادلة تفاضلية من الدرجة الثانية (معادلة تكون المشتقة الأعلى درجة بها مشتقةً ثانيةً) عدديًا حتى عندما لا نستطيع إيجاد حل بدلالة دوال مألوفة.