المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | رقم قياسي النسبي Relative Index Number |
 1375
 02:08 صباحاً
التاريخ: 10-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 145-146|
أقرأ أيضاً
التاريخ: 24-11-2015
23446
التاريخ: 16-12-2015
6549
التاريخ: 3-11-2015
2220
التاريخ: 22-12-2015
1532
|
هذا الرقم القياسي من الأرقام المستخدمة في الظواهر الاقتصادية لمقارنة عدة سلع في أزمنة متتالية أو امكنة متباينة .
ويتم حسابه بإيجاد الوسط الحسابي لجميع الأرقام القياسية للسلع المذكورة فإذا كان ع ر يمثل سعر السلعة سنة المقارنة .
وكان ع. يمثل سعر السلعة سنة الأساس .
فإن الرقم القياسي النسبي لعدد ك من السلع هو :
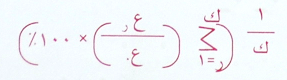
ومثال : إذا كانت أسعار سلع في سنتين كما يلي :
والتفسير ان السلع التي تم شراؤها عام 1980م بــ 100 دينار تحتاج لعام 1990م إلى 160 دينار .
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
