
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
?What is the force
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 9
2024-02-05
1949
In order to use Newton’s laws, we have to have some formula for the force; these laws say pay attention to the forces. If an object is accelerating, some agency is at work; find it. Our program for the future of dynamics must be to find the laws for the force. Newton himself went on to give some examples. In the case of gravity, he gave a specific formula for the force. In the case of other forces, he gave some part of the information in his Third Law, which we will study in the next chapter, having to do with the equality of action and reaction.
Extending our previous example, what are the forces on objects near the earth’s surface? Near the earth’s surface, the force in the vertical direction due to gravity is proportional to the mass of the object and is nearly independent of height for heights small compared with the earth’s radius R: F= GmM/R2= mg, where g=GM/R2 is called the acceleration of gravity. Thus, the law of gravity tells us that weight is proportional to mass; the force is in the vertical direction and is the mass times g. Again we find that the motion in the horizontal direction is at constant velocity. The interesting motion is in the vertical direction, and Newton’s Second Law tells us

Cancelling the m’s, we find that the acceleration in the x–direction is constant and equal to g. This is of course the well known law of free fall under gravity, which leads to the equations
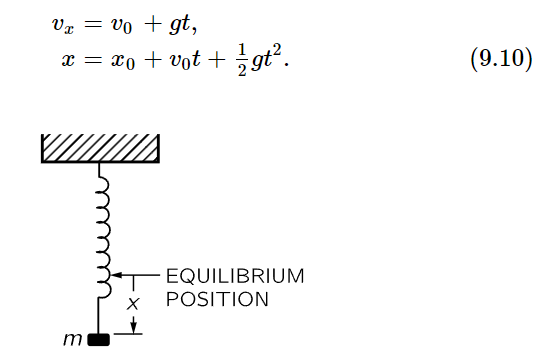
Fig. 9–3. A mass on a spring.
As another example, let us suppose that we have been able to build a gadget (Fig. 9–3) which applies a force proportional to the distance and directed oppositely—a spring. If we forget about gravity, which is of course balanced out by the initial stretch of the spring, and talk only about excess forces, we see that if we pull the mass down, the spring pulls up, while if we push it up the spring pulls down. This machine has been designed carefully so that the force is greater, the more we pull it up, in exact proportion to the displacement from the balanced condition, and the force upward is similarly proportional to how far we pull down. If we watch the dynamics of this machine, we see a rather beautiful motion—up, down, up, down, … The question is, will Newton’s equations correctly describe this motion? Let us see whether we can exactly calculate how it moves with this periodic oscillation, by applying Newton’s law (9.7). In the present instance, the equation is
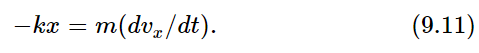
Here we have a situation where the velocity in the x–direction changes at a rate proportional to x. Nothing will be gained by retaining numerous constants, so we shall imagine either that the scale of time has changed or that there is an accident in the units, so that we happen to have k/m=1. Thus we shall try to solve the equation

To proceed, we must know what vx is, but of course we know that the velocity is the rate of change of the position.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















