في عام 1964، نشر جون بيل مقالة بعنوان (حول مفارقة أ. ب. ر) وفيها يعبر عن أرائه عما ورد في تلك النشرة بخصوص المتغيرات الخفية. يبدأ بل في مقالته بفرضيتين أساسيتين. الأولى، وجود قيم للكميات الفيزيائية لا علاقة للقياس بشأنها الثانية افتراض صحة علاقة التموضع. بمعنى أنه لا يمكن أن ينتقل التأثير بين أي جسيمان بشكل أني أو لحظي.

كانت الأفكار الواردة في نشرة أ. ب. ر، في البداية مجرد أفكار ذهنية. ما حاول بيل القيام به هو اختبار هذه التجربة فعليا. لذلك لم تنفذ هذه التجربة إلى في السنوات الأخيرة، بعدما تطورت التكنولوجيا بشكل كافي.

نعود الآن إلى البايون المتعادل الذي ينحل إلى فوتونين لهما كمية دوران مغزلي متعاكسة، إن التجارب التي أجريت لاختبار مفارقة أ. ب. ر، لم تعتمد على كمية الدوران المغزلي للفوتونات، بل اعتمدت على كمية أخرى تسمى الاستقطاب polarization. يمكن وصف الاستقطاب بالنسبة للضوء باتجاه المجال الكهربائي في الفضاء. فعندما ينتشر الضوء (موجات كهرومغناطيسية)، تكون خطوط المجال الكهربائي عمودية على اتجاه انتشاره في كل الاتجاهات، كما هو موضح بالشكل (2–6).

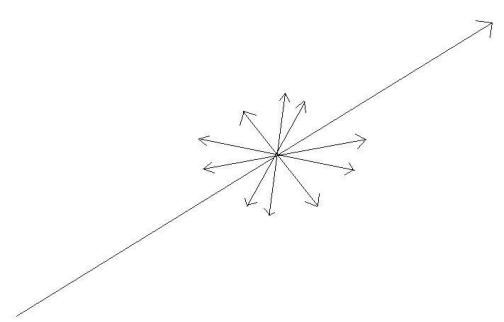
شكل (2–6)

تكون خطوط المجال الكهربائي عمودية على جهة انتشار الموجة الكهرومغناطيسية.

لكن إذا أردنا الحصول على خطوط مجال كهربائي تهتز وفق منحنى معين، نقوم بوضع ما يسمى (المقطب) polarizer. حيث يجعل هذا الأخير خطوط المجال الكهربائي تمر في منحنى خاص نقوم نحن بتحديده كما هو موضح بالشكل (3–6). هذا هو مبدأ عمل النظارات الشمسية.

لنفترض الآن بأنه لدينا مصدر من البايونات المشعة للفوتونات، ولنفترض كذلك بأن كل واحد من الفوتونات المنطلقة له اتجاه استقطاب إما إلى أعلى أوالى أسفل نضع الآن مقطبين في طريق كل من الفوتونين المنطلقين بحسب مبدأ حفظ الكميات، فأنه إذا ما علمنا عن حالة استقطاب أحد الفوتونين لدى وصوله إلى المقطب، سوف نعلم عن حالة الأخر بدون قياسه. مثلا، لو عبر الفوتون المتجه إلى المقطب (A) منه، فأننا نستنتج بأن الفوتون الذاهب إلى المقطب (B)، سوف يعبر هو الأخر، بدون إجراء أي قياس عليه. وإذا لم يعبر الفوتون الأول من المقطب (A)، فأن الفوتون الذاهب إلى المقطب (B) يجب ألا يعبر كذلك.

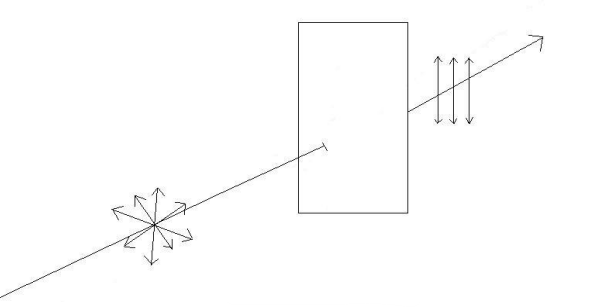
شكل (3–6)

استقطاب الضوء عند مروره داخل المقطب.

في البداية سنضع المقطبين بشكل متوازي مع كل من الفوتونين المنطلقين، كما هو موضح بالشكل (4–6). يوجد راصدان عند كل من المقطب (A) و(B)، حتى يخبرانا بحالة استقطاب كل من الفوتونين المنطلقين بشكل متعاكس. في هذه الحالة ستكون نتائج كلا الراصدين متطابقة تماما. هذا متوقع لأنه إذا كانت حالة استقطاب الفوتون المتجه إلى المقطب (A) عمودية، أي موازية لاتجاه المقطب فأن الفوتون سوف يعبر بهذا نكون قد علمنا عن حالة استقطاب الفوتون الذاهب إلى (B) قبل أن يقيسه الراصد الموجود هناك حتى الآن يسير كل شيء بشكل جيد. نقوم الآن باستدارة المقطب (B) بزاوية 45º مع محور المقطب (A)، كما هو موضح بالشكل (5–6).

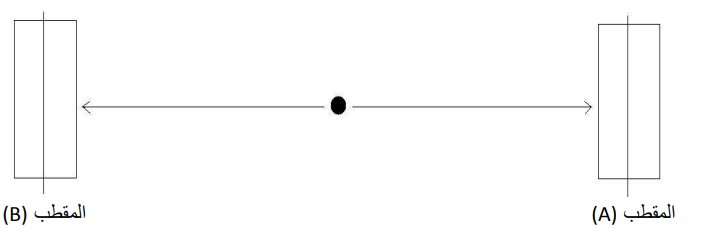
شكل (4–6)

يصدر المصدر المشع فوتونين متعاكسين، يذهبان إلى مقطبين في وضعية توازي مع اتجاه استقطاب كلا الفوتونين.

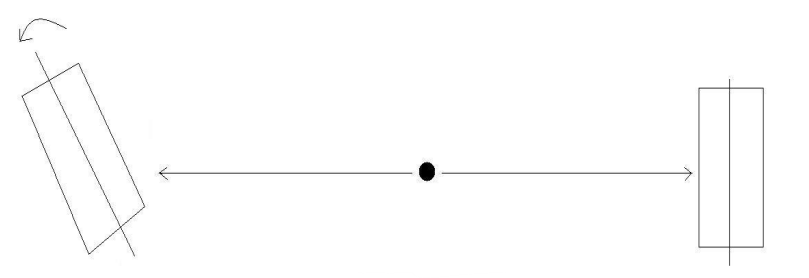
شكل (5–6)

ميلان المقطب (B) بزاوية 45º بالنسبة لمحور المقطب (A).

الآن إذا عبر الفوتون المتجه إلى المقطب (A) فأننا نكون قد علمنا بأن حالته قبل الوصول كانت عمودية، وبالتالي يجب أن تكون حالة الفوتون الذاهب إلى المقطب (B) أيضا عمودية، وبالتالي لن يعبر من المقطب، لان المقطب (B) مائل بزاوية 45º مع منحنى المقطب (A). لكن هذا ما افترضناه نظريا، إن التجربة تعطي نتائج أخرى. حيث سيجد الراصد الموجود عند المقطب (B) بأن نصف الفوتونات قد عبر، ونصفها الأخر لم يعبر؟!! أي أن هناك حالة تطابق بنسبة خمسون بالمائة بين نتائج الراصد (A) و(B). لماذا يمر بعض هذه الفوتونات ويمتنع بعضها الآخر؟ أليس من المفروض بأن لا يمر أي منها، لأننا قد علمنا عن حالتهما قبل عملية القياس.

كانت إحدى المحاولات الأولى لحل هذه المعضلة هي افتراض وجود ترابط أو تشابك بين كل من الفوتونين أو المقطبين. لكن نتيجة هذا الحل هو اختراق مبدأ أساسي، وهو عدم وجود إشارة تنتقل بأسرع من سرعة الضوء. نحن نعلم بأن الفوتونين لهما سرعة الضوء نفسها، وبالتالي صدور إشارة من المقطب (A) في حالة وصول الفوتون إليه إلى المقطب (B) ليعلمه بأن الفوتون الخاص به قد عبر أو لا، ستكون أسرع بكثير من سرعة الضوء. وهذا كما قلنا يتناقض مع مبدأ فيزيائي أساسي، وهو أن سرعة الضوء هي الحد الأعلى للسرعة في الكون. ما هو الحل إذن؟

الحل هو أن بور ورفاقه كانوا على حق في ادعائهم بأن الكميات المتغيرة ليست لها قيمة محددة قبل عملية القياس إن حالة استقطاب الفوتون الذاهب إلى المقطب (A) أو الذاهب إلى المقطب (B) ليس لها قيمة أو معنى محدد قبل الاصطدام بالمقطب فحالة استقطاب الفوتون قبل أن يصطدم بالمقطب عبارة عن تراكب من عدة حالات. لذلك نستطيع افتراضا بأن حالة استقطاب الفوتون قبل عملية القياس مكونة من موجتي احتمال، إحداهما موازية لمحور المقطب والأخرى عمودية عليه. الشكل (6–6) كل واحدة من هذه الموجتين لها شدة احتمال معينة، تكون هي المسؤولة عن احتمالية عبور الفوتون أو عدم عبوره. ففي الحالة الأولى، عندما كان اتجاه المقطبين متوازيان، شكل (4–6) كان سبب تطابق النتائج هو وضعية المقطبين نفسها. فوضعية المقطبين بشكل عمودي يزيد من فرصة عبور موجة الاحتمال العمودية بشكل كبير. لكن هذا لا يعني بأنه في كل مرة سوف يعبر كلا الفوتونين، فهناك احتمال أيضا، ولكن ضئيل جدا بأن لا يعبر الفوتونين. لكن يبقى الترابط بين الفوتونين موجودا في كل عملية قياس. إذن يحق لنا القول، بأن الراصد هو المسؤول عن تحديد ما إذا كان الفوتون سيعبر أو لا، وذلك عن طريق تحكمه بوضعية المقطب نفسها. لذلك عندما وضعنا المقطب (B) مائلا بزاوية 45º مع المقطب (A)، أصبحت فرصة عبور كلا موجتي الاحتمال العمودية والأفقية متساوية، أي خمسون بالمائة لكليهما. وهذا يفسر لنا لماذا خرجت نصف الفوتونات وامتنع النصف الأخر عن الخروج. وهكذا إذا قمنا بزيادة درجة ميلان المقطب (B) بزاوية أكثر من 45º، ستتغير شدة الاحتمال بحيث تزداد فرصة عبور موجة الاحتمال الأفقية أكثر، حتى إذا ما وصلت زاوية الميلان إلى 90º، تصبح فرصة عبور الموجة الأفقية كبيرة جدا.

هل تثبت يا ترى هذه التجربة صحة رأي مدرسة كوبنهاغن القائل بعدم وجود قيمة محددة للكميات الفيزيائية قبل عملية القياس؟ في الحقيقة لقد تقبل الفيزيائيين هذا الرأي الخيالي تدريجيا، وكثيرا منهم اليوم يعتنقون هذا الرأي، ويبدوا لي بالفعل أنه صحيح. لقد حاول اينشتاين ورفاقه وضع تجربة لتثبت صحة رأيهم، ولكن يبدو أن السحر قد انقلب على الساحر، وباتت تلك التجربة أعظم دليل ضدهم.

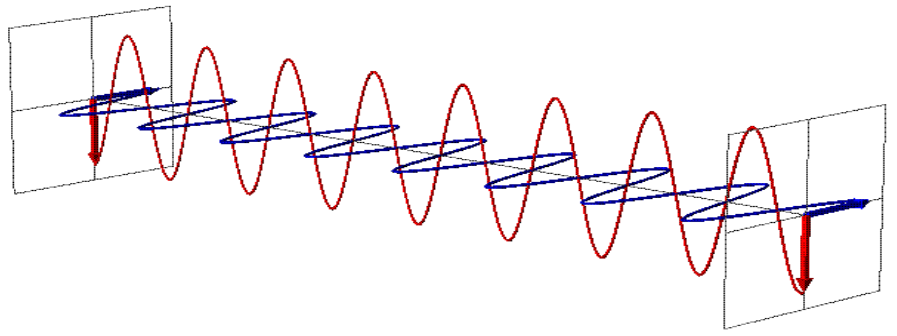
شكل (6–6)

لا يكون استقطاب الفوتون على حالة محددة قبل إجراء قياس عليه فهو مركب من موجتي احتمال، إحداهما موازية لمحور المقطب والأخرى عمودية عليه.