
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
بلانك يتفادى المشكلة أو يطلق أول رصاصة على الميكانيكا الكلاسيكية
المؤلف:
يوسف البناي
المصدر:
ميكانيكا الكم بين الفلسفة والعلم
الجزء والصفحة:
ص16–18
2023-10-14
2850
شكلت نظرية رايلي – جينز صدمة لمجتمع الفيزيائيين آنذاك، فعلى الرغم من استخدام قوانين الفيزياء الكلاسيكية والنظرية الكهرومغناطيسية لتفسير إشعاع الجسم الأسود، وافتراض أن هذا الإشعاع ناتج عن الحركة الاهتزازية للإلكترونات الموجودة في جدار الجسم، إلا أن كل ذلك لم ينجح في تفسير إشعاع الجسم الأسود فأين الخلل إذن؟ أفي النظرية أم في قوانين الفيزياء الكلاسيكية؟
في عام 1900، أتى ماكس بلانك ليجيب على هذا السؤال؟ لقد اكتشف بلانك أن الخطأ يكمن في استخدام رايلي وجينز متوسط الطاقة الكلية من المعادلة (7-1) كانت الملاحظة المهمة أن حساب متوسط الطاقة من هذه المعادلة الأخيرة يعتمد فقط على درجة الحرارة T. رياضيا نقول، طالما أن هذه المعادلة لا تعمل إلا في الطاقات المنخفضة جدا، إذن نستطيع كتابة أن:
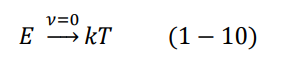
ولقد لاحظنا من قبل أن كثافة الطاقة الكلية لإشعاع الجسم الأسود، تزداد بزيادة التردد، حتى تصل إلى قيمة عظمى ثم تبدأ بعدها بالنزول السريع أي أن:
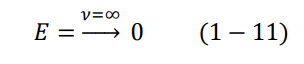
استنتج بلانك من ذلك أن متوسط الطاقة الكلية يجب أن يعتمد على التردد، لا على درجة الحرارة. لم يجد بلانك نفسه إلا أمام خيار واحد، وهو افتراض ان الطاقة الكلية للموجات الموقوفة لا تأخذ إلا قيما منفصلة من الطاقة. وهذا مخالف بشكل واضح لما جاءت به النظرية الكهرومغناطيسية من أن الطاقة دائما متصلة.
يتفق بلانك مع نظرية رايلي – جينز في أن سبب الموجات الموقوفة هي المهتزات التوافقية للجسيمات المشحونة الموجودة في جدار الجسم الأسود. لكن الاختلاف بينهما كان حول ماهية الاشعاع. نجد في نظرية رايلي – جينز أن الإشعاع متصل، بينما نجد في نظرية بلانك أن الاشعاع منفصل. طالما أن الإشعاع منفصل، إذن يجب أن يكون مسبب هذه الإشعاع هو الأخر منفصل أيضا. أي أن طاقة المهتزات الذرية في جدران الجسم الأسود يجب أن تأخذ قيما منفصلة. وجد بلانك أن قيمة هذه الطاقة تساوي:

بهذه المعادلة الصغيرة، أدخل بلانك الفيزياء إلى عهد جديد اذ مثلت هذه المعادلة ميلاد العصر الكمومي. لقد افترض بلانك ولأول مرة أن الطاقة تأخذ قيما منفصلة تسمى (كوانتا) Quanta. h الموجود في المعادلة أعلاه يسمى ثابت بلانك Plank's constant، ويعد الآن، على الرغم من قيمته الصغيرة جدا من أشهر الثوابت الفيزيائية، وقيمته تساوي:
h = 6.63 x 10–34 J.s
وn عدد صحيح أي ... ... ...، 3، 2، 1n =
نقوم الآن بتعويض المعادلة (12–1) في المعادلة (6–1) 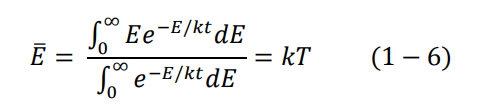

ونبدل التكاملات integrals إلى عملية الجمع sums. وهذا التبديل الرياضي ضروري حتى يتفق مع فكرة التقطيع التي اقترحها بلانك، فالتكامل رياضيا يعني الاستمرار وعملية الجمع تعني التقطيع. يتم الجمع لجميع المتذبذبات التوافقية، أي من 0 = n الى ∞n = حيث نجد
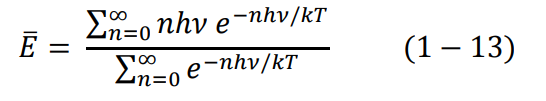
تستطيع رياضيا كتابة المعادلة السابقة كالتالي:

وتسمى هذه العلاقة الشهيرة بقانون بلانك لإشعاع الجسم الأسود وتتفق هذه العلاقة بصورة مذهلة مع النتائج التجريبية، كما هو موضح بالشكل (6–1).
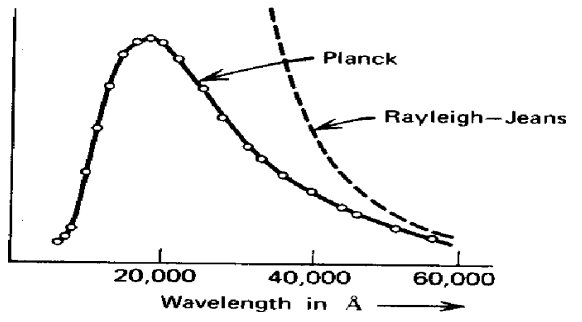
شكل (6–1)
مقارنة بين قانون بلانك ورايلي – جينز النتائج التجريبية (النقاط) تتفق بشكل مثير مع قانون بلانك.
لم يتنبأ قانون بلانك مع النتائج التجريبية وحسب، بل استطاع أن يبين بأن كل القوانين السابقة عليه، والتي حاولت تفسير إشعاع الجسم الأسود كانت حالة خاصة لقانونه. فلكي نحصل على قانون فين للإزاحة، نقوم باشتقاق المعادلة (16-1) ومن ثم نساويها بالصفر، وذلك لإيجاد القيمة العظمى، أي maxλ. ولإيجاد قانون ستيفان – بولتزمان، نقوم بتكامل المعادلة (16-1) على جميع الأطوال الموجية، ولكنه تكامل صعب بعض الشيء. أخيرا بالنسبة لقانون رايلي – جينز، فقد بينا فيما سبق أن متوسط الطاقة والذي استخدم من قبل رايلي وجينز، ولكن هذا القانون لا يتفق الا مع الترددات المنخفضة، أما في الحالة العامة فيجب استخدام قانون فين. نستطيع الآن كتابة العلاقة التالية في حالة الترددات المنخفضة:
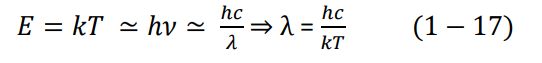
عندما تكون قيمة λ كبيرة جدا أي طاقة منخفضة v، سيؤدي ذلك الى تصغير قيمة e في المعادلة (16–1). وبعدها يمكننا استخدام التقريب الرياضي التالي:

حيث x = hv/kT، وبالتعويض في المعادلة (16-1) نحصل على قانون رايلي – جينز. إن قانون رايلي – جينز لا يحتوي على الثابت الكمومي لذلك في حالة الطاقات المنخفضة يكون التأثير الكمومي غير مهم، ويمكن استخدام قانون رايلي – جينز. أما عندما تبدأ طاقات الإشعاع بالارتفاع يبدأ التأثير الكمومي بالدخول ويلعب الثابت h دورا هاما وهذا هو جوهر الاختلاف بين النظريتان.
لا شك أن فكرة التكميم التي أدخلها بلانك إلى المجتمع الفيزيائي كانت دخيلة عليهم. لذلك لم تلاقي قبولا واسعا في البداية، بل إن بلانك نفسه أصبح متحفظا على نظريته. فلا يوجد شيء تجريبي يثبت أن الإشعاع الحراري يتصرف بشكل متقطع. إذ أن كل ما قام به هو بناء صرف لنظرية رياضية تتفق مع التجربة فحسب.
لكن الأوان قد فات، وهو بنظريته تلك قد أطلق أول رصاصة على الميكانيكا الكلاسيكية. لقد بدل فكرة الاستمرار المقبولة لدى جميع الفيزيائيين بفكرة التقطيع الدخيلة على مجتمعهم المتحفظ على عاداته وتقاليده.
بعد خمس أعوام من نظرية بلانك كان المجتمع الفيزيائي على موعد للقاء فيزيائي دخيل أخر يدعى ألبرت أينشتين Albert Einstein لم يحاول ذاك الدخيل إبطال أو برهنة نظرية الشخص الذي أصبح صديقه الحميم فيما بعد بل كل ما فعله هو استعارة المسدس منه وإطلاق الرصاصة الثانية على الميكانيكا الكلاسيكية.
 الاكثر قراءة في الفيزياء الذرية
الاكثر قراءة في الفيزياء الذرية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















