


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-1-2022
Date: 26-12-2021
Date: 26-12-2021
|
A partially ordered set (or poset) is a set taken together with a partial order on it. Formally, a partially ordered set is defined as an ordered pair 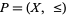 , where
, where 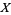 is called the ground set of
is called the ground set of 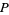 and
and 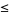 is the partial order of
is the partial order of 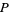 .
.
An element 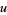 in a partially ordered set
in a partially ordered set 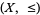 is said to be an upper bound for a subset
is said to be an upper bound for a subset 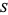 of
of 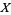 if for every
if for every 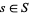 , we have
, we have 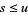 . Similarly, a lower bound for a subset
. Similarly, a lower bound for a subset 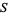 is an element
is an element 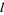 such that for every
such that for every 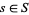 ,
, 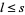 . If there is an upper bound and a lower bound for
. If there is an upper bound and a lower bound for 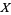 , then the poset
, then the poset 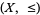 is said to be bounded.
is said to be bounded.
REFERENCES:
Dushnik, B. and Miller, E. W. "Partially Ordered Sets." Amer. J. Math. 63, 600-610, 1941.
Fishburn, P. C. Interval Orders and Interval Sets: A Study of Partially Ordered Sets. New York: Wiley, 1985.
Skiena, S. "Partial Orders." §5.4 in Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, pp. 203-209, 1990.
Trotter, W. T. Combinatorics and Partially Ordered Sets: Dimension Theory. Baltimore, MD: Johns Hopkins University Press, 1992.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
مكتب السيد السيستاني يعزي أهالي الأحساء بوفاة العلامة الشيخ جواد الدندن
|
|
|