


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-1-2022
Date: 27-12-2021
Date: 29-12-2021
|
Let 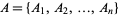 be a union-closed set, then the union-closed set conjecture states that an element exists which belongs to at least
be a union-closed set, then the union-closed set conjecture states that an element exists which belongs to at least 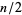 of the sets in
of the sets in 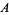 . Sarvate and Renaud (1989) showed that the conjecture is true if
. Sarvate and Renaud (1989) showed that the conjecture is true if 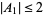 , where
, where 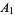 is the smallest set in
is the smallest set in 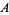 , or if
, or if 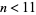 . They also showed that if the conjecture fails, then
. They also showed that if the conjecture fails, then 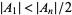 , where
, where 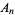 is the largest set of
is the largest set of 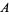 .
.
These results have since been improved for 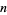 up to 18 (Sarvate and Renaud 1990), 24 (Lo Faro 1994a), 27 (Poonen 1992), 32 in (Gao and Yu 1998), and the best known result of 40 (Roberts 1992).
up to 18 (Sarvate and Renaud 1990), 24 (Lo Faro 1994a), 27 (Poonen 1992), 32 in (Gao and Yu 1998), and the best known result of 40 (Roberts 1992).
The proof for the case where 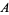 has a 2-set can be effected as follows. Write
has a 2-set can be effected as follows. Write 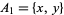 , then partition the sets of
, then partition the sets of 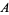 into four disjoint families
into four disjoint families 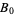 ,
, 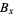 ,
, 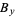 , and
, and 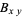 , according to whether their intersection with
, according to whether their intersection with 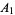 is
is 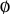 ,
, 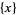 ,
, 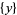 , or
, or 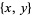 , respectively. It follows that
, respectively. It follows that 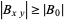 by taking unions with
by taking unions with 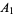 , where
, where 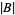 is the cardinal number of
is the cardinal number of 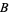 . Now compare
. Now compare 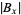 with
with 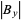 . If
. If 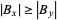 , then
, then 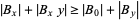 , so
, so  is in at least half the sets of
is in at least half the sets of 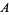 . Similarly, if
. Similarly, if 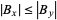 , then
, then 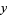 is in at least half the sets (Hoey, pers. comm.).
is in at least half the sets (Hoey, pers. comm.).
Unfortunately, this method of proof does not extend to 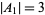 , since Sarvate and Renaud show an example of a union-closed set with
, since Sarvate and Renaud show an example of a union-closed set with 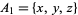 where none of
where none of  ,
, 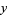 ,
, 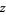 is in half the sets. However, in these cases, there are other elements which do appear in half the sets, so this is not a counterexample to the conjecture, but only a limitation to the method of proof given above (Hoey, pers. comm.).
is in half the sets. However, in these cases, there are other elements which do appear in half the sets, so this is not a counterexample to the conjecture, but only a limitation to the method of proof given above (Hoey, pers. comm.).
REFERENCES:
Gao, W. and Yu, H. "Note on the Union-Closed Sets Conjecture." Ars Combin. 49, 280-288, 1998.
Lo Faro, G. "A Note on the Union-Closed Sets Conjecture." J. Austral. Math. Soc. Ser. A 57, 230-236, 1994a.
Lo Faro, G. "Union-Closed Sets Conjecture: Improved Bounds." J. Combin. Math. Combin. Comput. 16, 97-102, 1994b.
Poonen, B. "Union-Closed Families." J. Combin. Theory Ser. A 59, 253-268, 1992.
Roberts, I. Tech. Rep. No. 2/92. School Math. Stat., Curtin Univ. Tech., Perth, 1992.
Sarvate, D. G. and Renaud, J.-C. "On the Union-Closed Sets Conjecture." Ars Combin. 27, 149-153, 1989.
Sarvate, D. G. and Renaud, J.-C. "Improved Bounds for the Union-Closed Sets Conjecture." Ars Combin. 29, 181-185, 1990.
West, D. "Union-Closed Sets Conjecture (1979)." http://www.math.uiuc.edu/~west/openp/unionclos.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|