


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-12-2021
Date: 5-1-2022
Date: 27-12-2021
|
In the theory of transfinite ordinal numbers,
1. Every well ordered set has a unique ordinal number,
2. Every segment of ordinals (i.e., any set of ordinals arranged in natural order which contains all the predecessors of each of its elements) has an ordinal number which is greater than any ordinal in the segment, and
3. The set 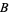 of all ordinals in natural order is well ordered.
of all ordinals in natural order is well ordered.
Then by statements (3) and (1), 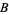 has an ordinal
has an ordinal 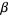 . Since
. Since 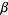 is in
is in 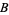 , it follows that
, it follows that 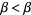 by (2), which is a contradiction.
by (2), which is a contradiction.
REFERENCES:
Burali-Forti, C. "Una questione sui numeri transfiniti." Rendiconti del Circolo Mat. di Palermo 11, 154-164, 1897.
Copi, I. M. "The Burali-Forti Paradox." Philos. Sci. 25, 281-286, 1958.
Curry, H. B. Foundations of Mathematical Logic. New York: Dover, p. 5, 1977.
Erickson, G. W. and Fossa, J. A. Dictionary of Paradox. Lanham, MD: University Press of America, pp. 29-30, 1998.
Mirimanoff, D. "Les antinomies de Russell et de Burali-Forti et le problème fondamental de la théorie des ensembles." Enseign. math. 19, 37-52, 1917.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|