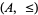Let  and 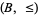 be disjoint totally ordered sets with order types  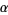and 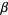. Then the ordinal sum is defined at set  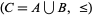where, if  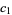and 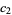 are both from the same subset, the order is the same as in the subset, but if  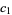is from  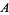and 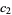 is from 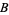, then  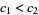has order type  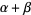(Ciesielski 1997, p. 48; Dauben 1990, p. 104; Moore 1982, p. 40).

One should note that in the infinite case, order type addition is not commutative, although it is associative. For example,

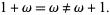(1)

In addition, {a} union {0,1,2,3,...}" src="https://mathworld.wolfram.com/images/equations/OrdinalAddition/Inline14.gif" style="height:15px; width:119px" />, with 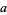 the least element, is order isomorphic to {0,1,2,3,...}" src="https://mathworld.wolfram.com/images/equations/OrdinalAddition/Inline16.gif" style="height:15px; width:84px" />, but not to {0,1,2,3,...} union {a}" src="https://mathworld.wolfram.com/images/equations/OrdinalAddition/Inline17.gif" style="height:15px; width:119px" />, with 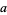 the greatest element, since it has a greatest element and the other does not.

An inductive definition for ordinal addition states that for any ordinal number ,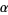

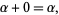(2)

and

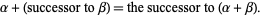(3)

If 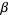 is a limit ordinal, then  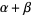is the least ordinal greater than any ordinal in the set {alpha+gamma:gamma<beta}" src="https://mathworld.wolfram.com/images/equations/OrdinalAddition/Inline22.gif" style="height:15px; width:80px" /> (Rubin 1967, p. 188; Suppes 1972, p. 205).

REFERENCES:

Ciesielski, K. Set Theory for the Working Mathematician. Cambridge, England: Cambridge University Press, 1997.

Dauben, J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1990.

Moore, G. H. Zermelo's Axiom of Choice: Its Origin, Development, and Influence. New York: Springer-Verlag, 1982.

Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.

Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد