


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-11-2021
Date: 18-12-2021
Date: 23-9-2021
|
Levenberg-Marquardt is a popular alternative to the Gauss-Newton method of finding the minimum of a function 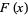 that is a sum of squares of nonlinear functions,
that is a sum of squares of nonlinear functions,
![F(x)=1/2sum_(i=1)^m[f_i(x)]^2.](https://mathworld.wolfram.com/images/equations/Levenberg-MarquardtMethod/NumberedEquation1.gif) |
Let the Jacobian of 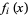 be denoted
be denoted 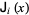 , then the Levenberg-Marquardt method searches in the direction given by the solution
, then the Levenberg-Marquardt method searches in the direction given by the solution 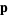 to the equations
to the equations
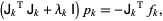 |
where 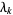 are nonnegative scalars and
are nonnegative scalars and 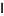 is the identity matrix. The method has the nice property that, for some scalar
is the identity matrix. The method has the nice property that, for some scalar 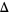 related to
related to 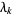 , the vector
, the vector 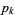 is the solution of the constrained subproblem of minimizing
is the solution of the constrained subproblem of minimizing 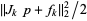 subject to
subject to 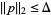 (Gill et al. 1981, p. 136).
(Gill et al. 1981, p. 136).
The method is used by the command FindMinimum[f,  x, x0
x, x0 ] when given the Method -> LevenbergMarquardt option.
] when given the Method -> LevenbergMarquardt option.
REFERENCES:
Bates, D. M. and Watts, D. G. Nonlinear Regression and Its Applications. New York: Wiley, 1988.
Gill, P. R.; Murray, W.; and Wright, M. H. "The Levenberg-Marquardt Method." §4.7.3 in Practical Optimization. London: Academic Press, pp. 136-137, 1981.
Levenberg, K. "A Method for the Solution of Certain Problems in Least Squares." Quart. Appl. Math. 2, 164-168, 1944.
Marquardt, D. "An Algorithm for Least-Squares Estimation of Nonlinear Parameters." SIAM J. Appl. Math. 11, 431-441, 1963.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|