


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2021
Date: 29-11-2021
Date: 6-10-2021
|
The central difference for a function tabulated at equal intervals 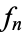 is defined by
is defined by
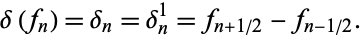 |
(1) |
First and higher order central differences arranged so as to involve integer indices are then given by
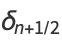 |
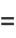 |
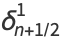 |
(2) |
 |
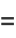 |
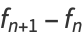 |
(3) |
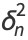 |
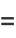 |
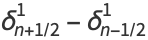 |
(4) |
 |
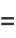 |
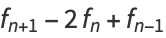 |
(5) |
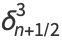 |
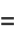 |
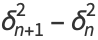 |
(6) |
 |
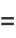 |
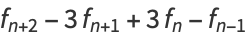 |
(7) |
(Abramowitz and Stegun 1972, p. 877).
Higher order differences may be computed for even and odd powers,
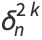 |
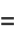 |
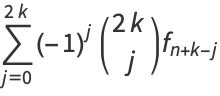 |
(8) |
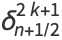 |
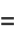 |
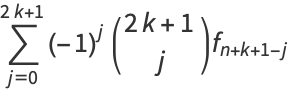 |
(9) |
(Abramowitz and Stegun 1972, p. 877).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Differences." §25.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 877-878, 1972.
Jeffreys, H. and Jeffreys, B. S. "Central Differences Formula." §9.084 in Methods of Mathematical Physics, 3rd ed. Cambridge, England: Cambridge University Press, pp. 284-286, 1988.
Sheppard, W. F. "Central-Difference Formulæ." Proc. London Math. Soc. 31, 449-488, 1899.
Whittaker, E. T. and Robinson, G. "Central-Difference Formulae." Ch. 3 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 35-52, 1967.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|