


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2021
Date: 22-9-2021
Date: 5-1-2016
|
Let 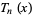 be an arbitrary trigonometric polynomial
be an arbitrary trigonometric polynomial
![T_n(x)=1/2a_0+{sum_(k=1)^n[a_kcos(kx)+b_ksin(kx)]}](https://mathworld.wolfram.com/images/equations/FavardConstants/NumberedEquation1.gif) |
(1) |
with real coefficients, let 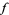 be a function that is integrable over the interval
be a function that is integrable over the interval ![[-pi,pi]](https://mathworld.wolfram.com/images/equations/FavardConstants/Inline3.gif) , and let the
, and let the 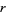 th derivative of
th derivative of 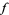 be bounded in
be bounded in ![[-1,1]](https://mathworld.wolfram.com/images/equations/FavardConstants/Inline6.gif) . Then there exists a polynomial
. Then there exists a polynomial 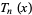 for which
for which
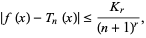 |
(2) |
for all ![x in [-pi,pi]](https://mathworld.wolfram.com/images/equations/FavardConstants/Inline8.gif) , where
, where 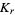 is the smallest constant possible, known as the
is the smallest constant possible, known as the 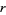 th Favard constant.
th Favard constant.
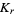 can be given explicitly by the sum
can be given explicitly by the sum
![K_r=4/pisum_(k=0)^infty[((-1)^k)/(2k+1)]^(r+1),](https://mathworld.wolfram.com/images/equations/FavardConstants/NumberedEquation3.gif) |
(3) |
which can be written in terms of the Lerch transcendent as
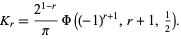 |
(4) |
These can be expressed by
 |
(5) |
where 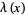 is the Dirichlet lambda function and
is the Dirichlet lambda function and 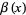 is the Dirichlet beta function. Explicitly,
is the Dirichlet beta function. Explicitly,
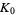 |
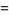 |
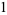 |
(6) |
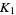 |
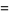 |
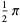 |
(7) |
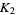 |
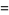 |
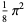 |
(8) |
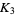 |
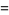 |
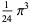 |
(9) |
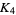 |
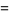 |
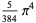 |
(10) |
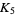 |
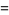 |
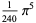 |
(11) |
(OEIS A050970 and A050971).
REFERENCES:
Finch, S. R. "Achieser-Krein-Favard Constants." §4. 2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 255-257, 2003.
Kolmogorov, A. N. "Zur Grössenordnung des Restgliedes Fourierscher reihen differenzierbarer Funktionen." Ann. Math. 36, 521-526, 1935.
Sloane, N. J. A. Sequences A050970 and A050970 in "The On-Line Encyclopedia of Integer Sequences."
Zygmund, A. G. Trigonometric Series, Vols. 1-2, 2nd ed. New York: Cambridge University Press, 1959.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|