المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Nash Equilibrium |
 1210
 05:47 مساءً
date: 5-11-2021 |
Author : Nash, J. F 
Book or Source : "Non-Cooperative Games." Ann. Math. 54 
Page and Part : 286-295|
Read More
Date: 22-12-2021
1609
Date: 23-11-2021
811
Date: 21-9-2021
931
|
A Nash equilibrium of a strategic game is a profile of strategies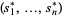 
, where 
(
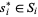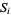is the strategy set of player 
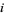), such that for each player 
, 
, 
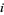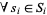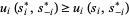, where 
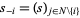and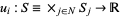 
.
Another way to state the Nash equilibrium condition is that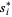 
solves 
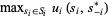for each 
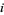. In words, in a Nash equilibrium, no player has an incentive to deviate from the strategy chosen, since no player can choose a better strategy given the choices of the other players.
The Season 1 episode "Dirty Bomb" (2005) of the television crime drama NUMB3RS mentions Nash equilibrium.
REFERENCES:
Nash, J. F. "Non-Cooperative Games." Ann. Math. 54, 286-295, 1951.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
